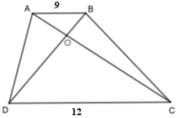
AB // CD nên ΔAOB ⁓ ΔCOD.
Tỉ số đồng dạng A O O C = B O O D = A B C D = 9 12 = 3 4 nên B, C đúng
Lại có: AB // CD nên A B D ^ = B D C ^ (so le trong nên D đúng
Đáp án A sai vì viết sai thứ tự các đỉnh của hai tam giác đồng dạng
Đáp án: A

AB // CD nên ΔAOB ⁓ ΔCOD.
Tỉ số đồng dạng A O O C = B O O D = A B C D = 9 12 = 3 4 nên B, C đúng
Lại có: AB // CD nên A B D ^ = B D C ^ (so le trong nên D đúng
Đáp án A sai vì viết sai thứ tự các đỉnh của hai tam giác đồng dạng
Đáp án: A
Hình thang ABCD AB || CD có AB = 10cm, CD = 25cm và hai đường chéo cắt nhau tại O. Chứng minhh rằng Δ A O B ∽ Δ C O D và tìm tỉ số đồng dạng
cho hình thang vuông ABCD (vuông tại A và D ) có 2 đường chéo vuông góc với nhau tại O , AB=4cm , CD=9cm.
a) CMR : tam giác OAB đồng dạng với tam giác DAB
b) Tính độ dài AD
c) CM : tam giác OAB đồng dạng với tam giác OCD
d) Tính tỉ số diện tích của tam giác OAB và OCD
Câu 3:Chứng minh rằng nếu tam giác A'B'C' đồng dạng với tam giác ABC theo tỉ số k thì tỉ số của hai đường trung tuyến tương ứng của hai tam giác đó cũng bằng tỉ số k
Câu 4:Cho hình thang ABCD (AB//CD) .Gọi O là gio điểm của hai đường chéo AC và BD
a) CMR: OA.OD=OB.OC
b) Đường thẳng qua O vuông góc với AB và CD theo thứ tự tại H vf K
CMR:OH/OK=AB/CD
Cho hình thang vuông ABCD ( góc A = góc D = 90), AB=4cm,CD=9cm,AD=6cm a) CM: tam giác BAD đồng dạng tam giác ADC b) CM: AC vuông góc với BD c) Gọi O là giao điểm của AC và BD. Tính tỉ số diện tích 2 hai tam giác AOB và COD. d) Gọi K là giao điểm của DA và CB. Tính KA.
Cho hình thang (AB // CD) có AB = 10 cm, CD = 25 cm, hai đường chéo cắt nhau tại O. Chứng minh rằng tam giác AOB đồng dạng với tam giác COD và tìm tỉ số đồng dạng.
Hình thang ABCD (AB // CD) có AB = 10cm, CD = 25cm, hai đường chéo cắt nhau tại O. Chọn khẳng định đúng.
A. ΔAOB ⁓ ΔCOD với tỉ số đồng dạng k = 2
B. A O O C = 2 3
C. ΔAOB ⁓ ΔCOD với tỉ số đồng dạng k = 2 5
D. ΔAOB ⁓ ΔCOD với tỉ số đồng dạng k = 5 2
Cho hình thang ABCD ( A B / / C D ) . Gọi O là giao điểm hai đường chéo AC và BD. Đường thẳng qua O và song song với hai đáy cắt AD tại E. Biết A B = 4 c m , C D = 6 c m . Tỉ số đồng dạng của hai tam giác AOE và ACD là:
A. 2 3
B. 12 5
C. 2 5
D. 4 5
Cho hình chữ nhật ABCD có AD = 6 cm , AB = 8 cm , hai đường chéo AC và BD cắt nhau tại O , Qua D kẻ đường thẳng d vuông góc với BD , d cắt tia BC tại E
a) Chứng minh rằng tam giác BDE đồng dạng với tam giác DCE
b) Kẻ CH vuông góc CE tại H , chứng minh rằng : DC^2 = CH * DB
c) Gọi K là giao điểm của OE và HC . Chứng minh rằng K là trung điểm của HC , và tính tỉ số diện tích của tam giác EHC và tam giác EDB
d) Chứng minh rằng ba đường thẳng OE , CD , BH đồng quy
Cho hình chữ nhật ABCD có AD = 6 cm , AB = 8 cm , hai đường chéo AC và BD cắt nhau tại O , Qua D kẻ đường thẳng d vuông góc với BD , d cắt tia BC tại E
a) Chứng minh rằng tam giác BDE đồng dạng với tam giác DCE
b) Kẻ CH vuông góc CE tại H , chứng minh rằng : DC^2 = CH * DB
c) Gọi K là giao điểm của OE và HC . Chứng minh rằng K là trung điểm của HC , và tính tỉ số diện tích của tam giác EHC và tam giác EDB
d) Chứng minh rằng ba đường thẳng OE , CD , BH đồng quy