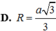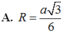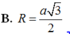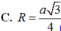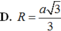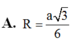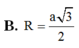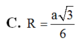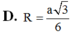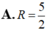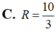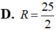Question

Hình chóp A'.BC'D có đáy ABC là tam giác vuông tại a, SA vuông góc với mặt phẳng (ABC), SA = a, AB = b, AC = c. Tính bán kính R của mặt cầu đi qua các điểm A, B, C và S ?

A. R = 2 ( a + b + c ) 3  

B.  R = 2 a 2 + b 2 + c 2

C.  R = 1 2 a 2 + b 2 + c 2

D.  R = a 2 + b 2 + c 2

Answer 1

Đáp án C

Hướng dẫn giải:

Gọi H, K lần lượt là trung điểm của BC và SA.

Dựng đường thẳng d đi qua H và vuông góc với (ABC). Khi đó d//SA.

Trong mặt phẳng (SAH) dựng đường thằng d 1  đi qua K và vuông góc với SA.

Khi đó,  d 1 //AH.

Gọi I = d ∩ d 1  tại. Ta có được IA = IB = IC = IS.

Khi đó mặt cầu cần tìm ở đề bài đi qua các điểm A, B, C, S có tâm là I và bán kính là R = IA.

Dễ thấy A H = 1 2 B C = b 2 + c 2 2

và I H = 1 2 S A = a 2 .

Trong ∆ I A H có

Vậy là ta hoàn thành xong bài toán.