Hình trụ có bán kính đáy bằng r và chiều cao bằng 2r
Vậy thể tích của nó là: ![]()
Hình trụ có bán kính đáy bằng r và chiều cao bằng 2r
Vậy thể tích của nó là: ![]()
Hình 120 mô tả một hình cầu được đặt khít vào trong một hình trụ, các kích thước cho trên hình vẽ.
Hãy tính: Hiệu giữa thể tích hình trụ và thể tích hình cầu.
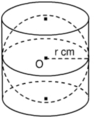
Hình 120
Hình 120 mô tả một hình cầu được đặt khít vào trong một hình trụ, các kích thước cho trên hình vẽ.
Hãy tính: Thể tích hình cầu.
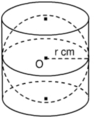
Hình 120
Hình 120 mô tả một hình cầu được đặt khít vào trong một hình trụ, các kích thước cho trên hình vẽ.
Hãy tính: Thể tích của một hình nón có bán kính đường tròn đáy là r cm và chiều cao 2r cm
Hình 120 mô tả một hình cầu được đặt khít vào trong một hình trụ, các kích thước cho trên hình vẽ.
Hãy tính:
a) Thể tích hình cầu.
b) Thể tích hình trụ.
c) Hiệu giữa thể tích hình trụ và thể tích hình cầu.
d) Thể tích của một hình nón có bán kính đường tròn đáy là r cm và chiều cao 2r cm.
e) Từ các kết quả a), b), c), d) hãy tìm mối liên hệ giữa chúng.
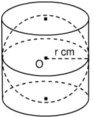
Hình 120
Hình 120 mô tả một hình cầu được đặt khít vào trong một hình trụ, các kích thước cho trên hình vẽ.
Hãy tính: Từ các kết quả a), b), c), d) hãy tìm mối liên hệ giữa chúng.
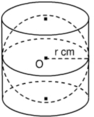
Hình 120
Một hình trụ được “đặt khít” vào bên trong một hình cầu bán kính r = 12cm như hình 112. Hãy tính: Thể tích hình cầu.
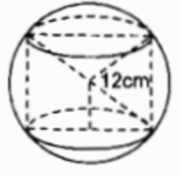
Một hình trụ được “đặt khít” vào bên trong một hình cầu bán kính r = 12cm như hình 112. Hãy tính: Diện tích mặt cầu.
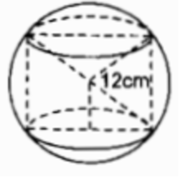
Một hình trụ được “đặt khít” vào bên trong một hình cầu bán kính r = 12cm như hình 112. Hãy tính: Diện tích xung quanh của hình trụ, biết chiều cao của hình trụ bằng đường kính đáy của nó.
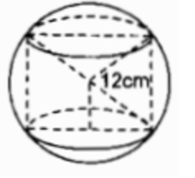
Một hình cầu đặt vừa khít vào trong một hình trụ như hình bên (chiều cao của hình trụ bằng độ dài đường kính của hình cầu) thì thể tích của nó bằng 2/3 thể tích của hình trụ.
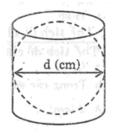
Nếu đường kính của hình cầu là d (cm) thì thể tích của hình trụ là:
A. (1/4). πd 3 cm 3 B. (1/3). πd 3 cm 3
C.(2/3). πd 3 cm 3 D. (3/4). πd 3 cm 3