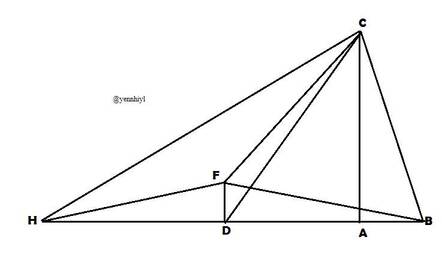
Gọi `D` là trung điểm của `BH`
Kẻ `DF` vuông góc `AB` tại `D;DF=AB`
Xét `\triangleFDB` và `\triangleBAC`:
`DF=AB`
`\hat{FDB}=\hat{BAC}=90^o`
`DB=AC`
`=>\triangleFDB=\triangleBAC{c.g.c)`
`=>FB=BC;\hat{FBD}=\hat{BCA}`
`=>\hat{FBD}=90^o - \hat{ABC}=15^o`
`=>\hat{FBC}=\hat{ABC} - \hat{FBD} = 60^o`
Xét `\triangleBFC`, có: `FB=BC=>\triangleBFC` cân tại `B`
Mà `\hat{FBC}=60^o =>\triangleBFC` đều
`=>FC=FB=BC` (*)
Ta có: `F\in` trung trực `BH=>FH=FB` (**)
Từ (*)(**)`=>FH=FC=FB`
Xét `\triangleHFB`, có: `FH=FB=>\triangleHFB` cân tại `F`
Mà `\hat{HBF}=15^o =>\hat{HFB}=180^o -2\hat{HBF}=150^o`
Ta có: `\hat{HFC} + \hat{HFB} + \hat{BFC} = 360^o`
`=>\hat{HFC}=360^o - 150^o - 60^o`
`=>\hat{HFC}=\hat{HFB}=150^o`
Xét `\triangleHFC` và `\triangleHFB`:
`HF` chung
`FC=FB`
`\hat{HFC}=\hat{HFB}`
`=>\triangleHFC=\hat{HFB}(c.g.c)`
`=>\hat{FHC}=\hat{FHB}`
`=>\hat{BHC}=2\hat{FHB}=2\hat{FBH}=30^o`
`=>\hat{BHC}=30^o`
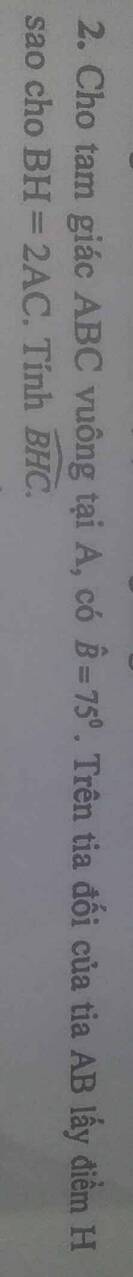


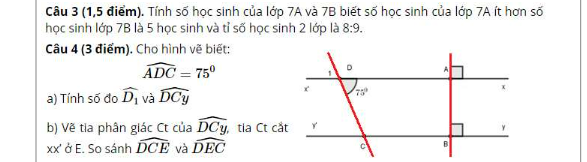



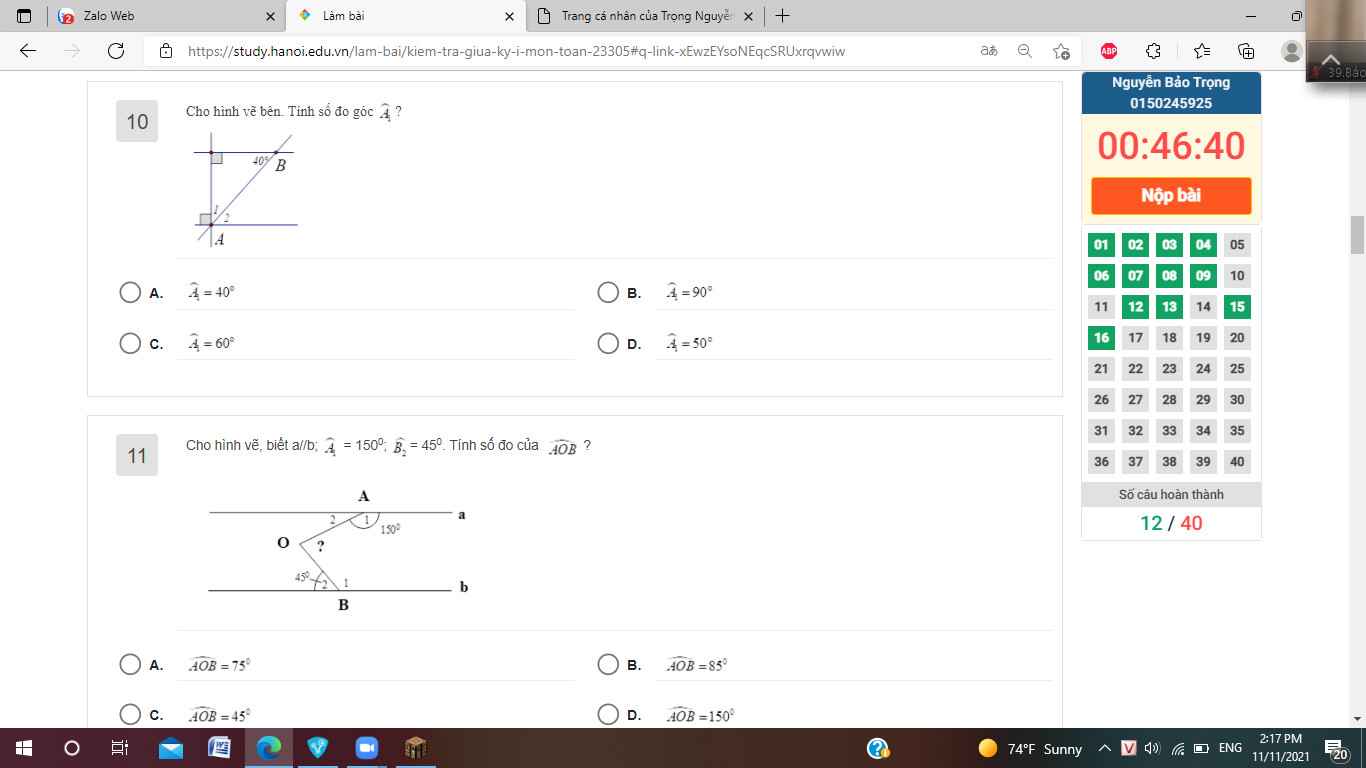

 Help mik bài 4 nha
Help mik bài 4 nha