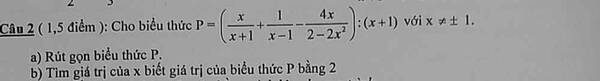`(x-2)^2/12-(x+1)^2/21=[(x-4)(x-6)]/28`
`<=> [7(x^2-4x+4)]/84-[4(x^2+2x+1)]/84=[3(x^2-6x-4x+24)]/84`
`=>7x^2 -28x+28 - 4x^2 -8x-4 = 3x^2- 18x -12x +72`
`<=> 7x^2 -28x -4x^2 -8x +18x +12x -3x^2 =72-28+4`
`<=>-6x = 48
`<=> x = -8`
Vậy `S={-8}`
\(\dfrac{\left(X-2\right)^2}{12}\)- \(\dfrac{\left(X+1\right)^2}{21}\)=\(\dfrac{\left(X-4\right)\left(X+6\right)}{28}\)
<=> \(\dfrac{7\left(X-2\right)^2}{84}\)-\(\dfrac{4\left(X+1\right)^2}{84}\)=\(\dfrac{3\left(X-4\right)\left(X-6\right)}{84}\)
<=>7(x-2)2 - 4(x+1)2 = 3(x-4)(x-6)
<=>7(x2 - 4x + 4) - 4(x2 + 2x + 1) = 3(x2 - 10x + 24)
<=>7x2 - 28x + 28 - 4x2 - 8x - 4 = 3x2 -30x +72
<=>7x2 - 4x2 - 3x2 - 28x - 8x + 30x = - 28 + 4 + 72
<=> 50x = 48
<=> x = \(\dfrac{48}{50}\)
<=> x = \(\dfrac{24}{25}\)
S = \(\left\{\dfrac{24}{25}\right\}\)
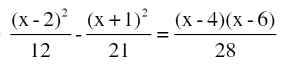


 cíu :((
cíu :(( cíu iem zới
cíu iem zới help me
help me