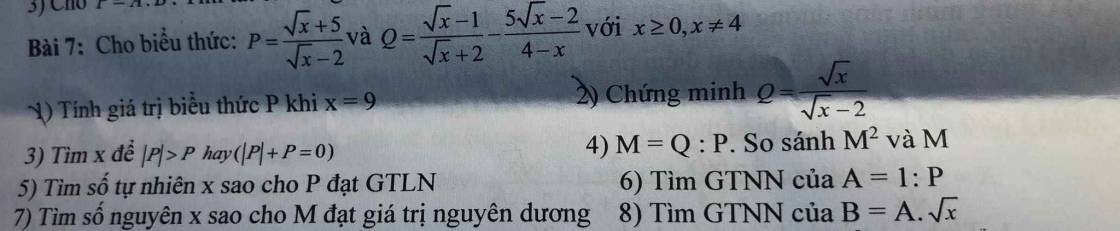1, Với x = 9
\(P=\dfrac{3+5}{3-2}=8\)
2, Với x >= 0 ; x khác 4
\(Q=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}-2\right)+5\sqrt{x}-2}{x-4}=\dfrac{x+2\sqrt{x}}{x-4}=\dfrac{\sqrt{x}}{\sqrt{x}-2}\)
Ta có đpcm
3, Ta có P > P (loại) hoặc -P > P
\(-\dfrac{\sqrt{x}+5}{\sqrt{x}-2}>\dfrac{\sqrt{x}+5}{\sqrt{x}-2}\Leftrightarrow\dfrac{2\left(\sqrt{x}+5\right)}{\sqrt{x}-2}< 0\)do tử > 0
\(\sqrt{x}-2< 0\Leftrightarrow x< 4\)
Kết hợp đk vậy 0 =< x < 4
4, Ta có \(M=Q:P=\dfrac{\sqrt{x}}{\sqrt{x}-2}.\dfrac{\sqrt{x}-2}{\sqrt{x}+5}=\dfrac{\sqrt{x}}{\sqrt{x}+5}\)
Ta có \(M^2-M=\dfrac{x}{\left(\sqrt{x}+5\right)^2}-\dfrac{\sqrt{x}}{\left(\sqrt{x}+5\right)}=\dfrac{x-\sqrt{x}\left(\sqrt{x}+5\right)}{\left(\sqrt{x}+5\right)^2}=\dfrac{-5\sqrt{x}}{\left(\sqrt{x}+5\right)^2}< 0\Rightarrow M^2< M\)
5, \(Q=\dfrac{\sqrt{x}}{\sqrt{x}-2}=\dfrac{\sqrt{x}-2+2}{\sqrt{x}-2}=1+\dfrac{2}{\sqrt{x}-2}\)
Ta có x >= 0 => \(\sqrt{x}-2\ge-2\Rightarrow\dfrac{2}{\sqrt{x}-2}\le-1\Leftrightarrow1+\dfrac{2}{\sqrt{x}-2}\le0\)
Dấu ''='' xảy ra khi x = 0
6, \(A=\dfrac{\sqrt{x}-2}{\sqrt{x}+5}=\dfrac{\sqrt{x}+5-7}{\sqrt{x}+5}=1-\dfrac{7}{\sqrt{x}+5}\)
x >= 0 => \(\sqrt{x}+5\ge5\Rightarrow\dfrac{-7}{\sqrt{x}+5}\ge-\dfrac{7}{5}\Rightarrow1-\dfrac{7}{\sqrt{x}+5}\ge-\dfrac{2}{5}\)
Dấu ''='' xảy ra khi x = 0
7,M = \(\dfrac{\sqrt{x}}{\sqrt{x}+5}=\dfrac{\sqrt{x}+5-5}{\sqrt{x}+5}=1-\dfrac{5}{\sqrt{x}+5}\)
Vì M đạt giá trị nguyên dương mà 1 nguyên nên 5/(căn x +5) nguyên
\(\sqrt{x}+5\inƯ\left(5\right)=\left\{1;5\right\}\)
| \(\sqrt{x}+5\) | 1 | 5 |
| x | loại | 0 |
8, Ta có \(B=\dfrac{x-2\sqrt{x}}{\sqrt{x}+5}\)
\(\Leftrightarrow B\sqrt{x}+5B=x-2\sqrt{x}\Leftrightarrow x-\sqrt{x}\left(B+2\right)+5B=0\)
Đặt \(\sqrt{x}=t\left(t\ge0\right)\)
\(t^2-t\left(B+2\right)+5B=0\)
\(\Delta=\left(B+2\right)^2-4.5B=B^2+4B+4-20B\)
\(=B^2-16B+4=B^2-16B+64-60=\left(B-8\right)^2-60\ge-60\)
Dấu ''='' xảy ra khi B = 8
bn giải nốt tìm x nhé