Từ bất đẳng thức Cô- si:
√xy ≤ (x + y)/2 ⇔ x + y ≥ 2√xy với x,y > 0
Dấu bằng xảy ra khi x = y
Do tích xy không đổi nên 2√xy không đổi ⇒ Tổng x + y nhỏ nhất khi và chỉ khi x = y
Từ bất đẳng thức Cô- si:
√xy ≤ (x + y)/2 ⇔ x + y ≥ 2√xy với x,y > 0
Dấu bằng xảy ra khi x = y
Do tích xy không đổi nên 2√xy không đổi ⇒ Tổng x + y nhỏ nhất khi và chỉ khi x = y
Hãy chứng minh 1+1=3
Chứng minh các hệ thức sau
Cho nửa hình tròn tâm O có đường kính AB=2R. Gọi M và N là hai điểm thuộc nửa đường tròn sao cho hai dây cung AM và BN cắt nhau tại I.
a) Chứng minh 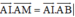 và
và 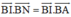
b) Hãy dùng kết quả câu a) để tính 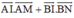 theo R.
theo R.
Phương trình hệ quả của phương trình x 2 - 3 = 0 là:
A . x 3 + x 2 - 3 x - 3 = 0
B . x 3 + x 2 - 6 x - 6 = 0
C . x 3 - 3 = 0
D . x 2 - 3 x = 0
Không sử dụng máy tính, hãy chứng minh:
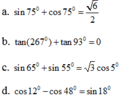
1.\(\)chứng minh hệ thức: \(\dfrac{sin\alpha+sin3\alpha+sin5\alpha}{cos\alpha+cos3\alpha+cos5\alpha}=tan3\alpha\)
2.rút gọn biểu thức: \(\dfrac{1+sin4\alpha-cos4\alpha}{1+cos4\alpha+sin4\alpha}\)
3. Tính \(96\sqrt{3}sin\dfrac{\pi}{48}cos\dfrac{\pi}{48}cos\dfrac{\pi}{24}cos\dfrac{\pi}{12}cos\dfrac{\pi}{6}\)
4. chứng minh rằng trong một △ABC ta có:
tanA + tanB + tanC = tanA tanB tanC (A,B,C cùng khác \(\dfrac{\pi}{2}\))
Cho tam giác $A B C$. Hai điểm $M, N$ được xác định bởi hệ thức $\overrightarrow{B C}+\overrightarrow{M A}=\overrightarrow{0}$, $\overrightarrow{A B}-\overrightarrow{N A}-3 \overrightarrow{A C}=\overrightarrow{0}$. Chứng minh rằng $M N / / A C$.
Cho tam giác ABC có M là trung điểm của trung tuyến AD, N là điểm thỏa mãn hệ thức: 3vecto AN=vectoAC
a) Chứng minh rằng 3 điểm B, M, N thẳng hàng.
b) Trên AB lấy điểm I sao cho vecto AI=2/3AB, trên AC lấy điểm J sao cho vecto AJ=2/5 vecto AC .
Chứng minh rằng 3 điểm I, M, J thẳng hàng.
giúp em làm phần b với ạ,,em cần gấp ạ
Hãy chứng minh công thức sin(a + b) = sina cosb + cosa sinb.