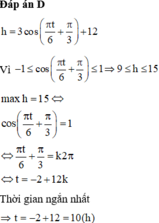Các câu hỏi tương tự
Hằng ngày mực nước của con kênh lên xuống theo thủy triều độ sâu h(m) của mực nước trong kênh tính theo thời gian t(h) trong ngày cho bởi công thức \(h=3\cos\left(\dfrac{\pi t}{6}+\dfrac{\pi}{3}\right)+12\) Khi nào mực nước của kênh là cao nhất với thời gian ngắn nhất?
thầy giải tự luận cho em hiểu được ko ạ. em cảm ơn nhiều ạ
Hằng ngày mực nước của con kênh lên xuống theo thủy triều. Độ sâu h(mét) của mực nước trong kênh được tính tại thời điểm t (giờ) trong một ngày bởi công thức
h
3
cos
π
t
8
+
π
4
+
12
Mực nước của kênh cao nhất khi? A. t 13 (giờ) B. t 14 (giờ) C. t 15 ...
Đọc tiếp
Hằng ngày mực nước của con kênh lên xuống theo thủy triều. Độ sâu h(mét) của mực nước trong kênh được tính tại thời điểm t (giờ) trong một ngày bởi công thức h = 3 cos π t 8 + π 4 + 12 Mực nước của kênh cao nhất khi?
A. t = 13 (giờ)
B. t = 14 (giờ)
C. t = 15 (giờ).
D. t = 16 (giờ)
Hằng ngày, mực nước của một con kênh lên xuống theo thủy triều. Độ sâu h (mét) của mực nước trong kênh tính theo thời gian t (giờ) trong một ngày
0
≤
t
24
cho bởi công thức
h
2
.
sin
3
πt
4
1
...
Đọc tiếp
Hằng ngày, mực nước của một con kênh lên xuống theo thủy triều. Độ sâu h (mét) của mực nước trong kênh tính theo thời gian t (giờ) trong một ngày 0 ≤ t < 24 cho bởi công thức h = 2 . sin 3 πt 4 1 - 4 . sin 2 πt 14 + 12 . Hỏi trong một ngày có bao nhiêu lần mực nước trong kênh đạt độ sâu 13m.
A. 5 lần
B. 7 lần.
C. 9 lần.
D. 9 lần.
Gọi a, b, c lần lượt là ba kích thước của một khối hộp chữ nhật (H) và V là thể tích của khối hộp chữ nhật (H). Khi đó V được tính bởi công thức:
Đọc tiếp
Gọi a, b, c lần lượt là ba kích thước của một khối hộp chữ nhật (H) và V là thể tích của khối hộp chữ nhật (H). Khi đó V được tính bởi công thức:
![]()
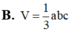
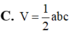
![]()
Cho biết điện lượng truyền trong dây dẫn theo thời gian biểu thị bởi hàm số Q ( t ) = 2 t 2 + t , trong đó t được tính bằng giây (s) và Q được tính theo Culong (C). Tính cường độ dòng điện tại thời điểm t=4s.
A. 13
B. 16
C. 36
D. 17
Cho khối nón cụt có R, r lần lượt là bán kính hai đáy và h3 là chiều cao. Biết thể tích khối nón cụt là
V
π
tìm giá trị lớn nhất của biểu thức PR+2r A.
2
3
B. 3. C.
3
3
D. 2.
Đọc tiếp
Cho khối nón cụt có R, r lần lượt là bán kính hai đáy và h=3 là chiều cao. Biết thể tích khối nón cụt là V = π tìm giá trị lớn nhất của biểu thức P=R+2r
A. 2 3
B. 3.
C. 3 3
D. 2.
Cho mặt cầu (S) tâm O, bán kính R. Xét mặt phẳng (P) thay đổi cắt mặt cầu theo giao tuyến là đường tròn (C) Hình trụ (T) nội tiếp mặt cầu (S) có một đáy là đường tròn (C)và có chiều cao là h(h0) Tính h để khối trụ (T) có giá trị lớn nhất
Đọc tiếp
Cho mặt cầu (S) tâm O, bán kính R. Xét mặt phẳng (P) thay đổi cắt mặt cầu theo giao tuyến là đường tròn (C) Hình trụ (T) nội tiếp mặt cầu (S) có một đáy là đường tròn (C)và có chiều cao là h(h>0) Tính h để khối trụ (T) có giá trị lớn nhất
![]()
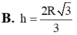
![]()
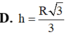
Cho hình lăng trụ ABC.ABC có mặt đáy ABC là tam giác đều, độ dài cạnh AB 2a. Hình chiếu vuông góc của A lên (ABC) trùng với trung điểm H của cạnh AB. Biết góc giữa cạnh bên và mặt đáy bằng
60
0
, tính theo a khoảng cách h từ điểm B đến mặt phẳng (ACCA)
A
.
h
39
a
13
B
.
...
Đọc tiếp
Cho hình lăng trụ ABC.A'B'C' có mặt đáy ABC là tam giác đều, độ dài cạnh AB = 2a. Hình chiếu vuông góc của A' lên (ABC) trùng với trung điểm H của cạnh AB. Biết góc giữa cạnh bên và mặt đáy bằng 60 0 , tính theo a khoảng cách h từ điểm B đến mặt phẳng (ACC'A')
A . h = 39 a 13
B . h = 2 15 a 5
C . h = 2 21 a 7
D . h = 15 a 5
Từ độ cao 63m của tháp nghiêng PISA ở Italia (H.5) người ta thả một quả bóng cao su xuống đất. Giả sử mỗi lần chạm đất quả bóng lại nảy lên một độ cao bằng 1/10 độ cao mà quả bóng đạt được ngay trướcđó.Tính độ dài hành trình của quả bóng từ thờiđiểm ban đầu cho đến khi nó nằm yên trên mặt đất.
Đọc tiếp
Từ độ cao 63m của tháp nghiêng PISA ở Italia (H.5) người ta thả một quả bóng cao su xuống đất. Giả sử mỗi lần chạm đất quả bóng lại nảy lên một độ cao bằng 1/10 độ cao mà quả bóng đạt được ngay trướcđó.
Tính độ dài hành trình của quả bóng từ thờiđiểm ban đầu cho đến khi nó nằm yên trên mặt đất.