Đáp án D
Quay trở lại tính chất của hàm số mũ
Ta thấy 0 < π + 3 2 π < 1 (do 3 < π ) nên hàm số y = π + 3 2 π x nghịch biến trên tập xác định của nó.
Đáp án D
Quay trở lại tính chất của hàm số mũ
Ta thấy 0 < π + 3 2 π < 1 (do 3 < π ) nên hàm số y = π + 3 2 π x nghịch biến trên tập xác định của nó.
Cho hàm số f(x)=3 sinx+2. Gọi S là tập hợp các giá trị nguyên của tham số m để hàm số y = f 3 ( x ) - 3 mf 2 ( x ) + 3 ( m 2 - 4 ) f ( x ) - m nghịch biến trên khoảng (0;π/2). Số tập con của S bằng
A. 1
B. 2.
C. 4.
D. 16.
Hàm số y=f(x) có đạo hàm f ' ( x ) = x ( x - 1 ) 2 ( x - 2 ) , ∀ x ∈ R . Hàm số y=f(x) nghịch biến trên khoảng nào dưới đây ?
A. ( 2 ; + ∞ ) .
B. (0;2).
C. ( - ∞ ; 0 ) .
D. ( 1 ; + ∞ ) .
Cho hàm số f(x) có đồ thị của hàm số y=f'(x) như hình vẽ bên và f(-2)=f(2)=0. Hàm số y = ( f ( 3 - x ) ) 2 nghịch biến trên khoảng nào dưới đây ?
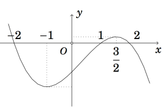
A. (1;2).
B. (-2;-1).
C. ( 5 ; + ∞ ) .
D. (2;5).
Cho hàm số f(x) có bảng biến thiên như sau:
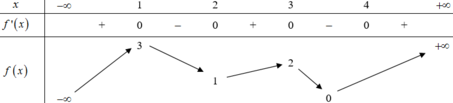
Hàm số y = ( f ( x ) ) 3 - 3 ( f ( x ) ) 2 nghịch biến trên khoảng nào dưới đây?
A. (2;3).
B. (1;2).
C. (3;4).
D. (-∞;1).
Cho hàm số y=f(x) có bảng biến thiên như sau
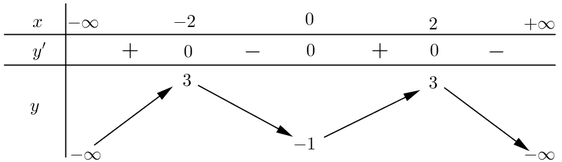
Hàm số y=f(x^2-2) nghịch biến trên khoảng nào dưới đây ?
A. (-2;0).
B. ( 2 ; + ∞ ) .
C. (0;2).
D. ( - ∞ ; - 2 ) .
Cho hàm số f(x) có đồ thị của hàm số y=f’(x-2)+2 như hình vẽ dưới. Hàm số y=f(x) nghịch biến trên khoảng nào dưới đây?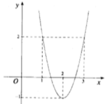
![]()
![]()
![]()
![]()
Cho hàm số y=f(x) có bảng xét dấu của đạo hàm như sau.
x -∞ -2 -1 2 4 +∞
f’(x) + 0 - 0 + 0 - 0 +
Hàm số y =-2f(x)+2019 nghịch biến trên khoảng nào trong các khoảng dưới đây?
A. (-4 ;2)
B. (-1 ;2)
C. (-2 ;-1)
D. (2 ;4)
Hàm số y=x^4 -2 nghịch biến trên khoảng nào dưới đây?
A. 1 2 ; + ∞
B. 0 ; + ∞
C. - ∞ ; 0
D. - ∞ ; 1 2
Cho hàm số f (x) có đồ thị của hàm số y = f'(x-2)+2 như hình vẽ bên.
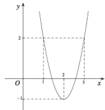
Hàm số y = f(x) nghịch biến trên khoảng nào dưới đây ?
A. - ∞ ; 2
B. - 1 ; 1
C. 3 2 ; 5 2
D. 2 ; + ∞
Cho hàm số f (x) có đồ thị của hàm số y=f'(x-2)+2 như hình vẽ bên.
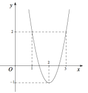
Hàm số y=f(x) nghịch biến trên khoảng nào dưới đây ?
A. ( - ∞ ; 2 ) .
B. (-1;1).
C. 3 2 ; 5 2 .
D. ( 2 ; + ∞ ) .