Các câu hỏi tương tự
Cho các mệnh đề sau đây:(1) Hàm số
f
(
x
)
log
2
2
x
-
log
2
x
4
+
4
có tập xác định
D
[
0
;
+
∞
)
(2) Hàm số
y
log
a
x
có tiệm cận ngang(3) Hàm số
y
log
a
x
;
...
Đọc tiếp
Cho các mệnh đề sau đây:
(1) Hàm số f ( x ) = log 2 2 x - log 2 x 4 + 4 có tập xác định D = [ 0 ; + ∞ )
(2) Hàm số y = log a x có tiệm cận ngang
(3) Hàm số y = log a x ; 0 < a < 1 và Hàm số y = log a x , a > 1 đều đơn điệu trên tập xác định của nó
(4) Bất phương trình: log 1 2 5 - 2 x 2 - 1 ≤ 0 có 1 nghiệm nguyên thỏa mãn.
(5) Đạo hàm của hàm số y = ln 1 - cos x là sin x 1 - cos x 2
Hỏi có bao nhiêu mệnh đề đúng:
A. 0
B. 2
C. 3
D.1
Cho hàm số
y
(
x
-
2
)
-
1
2
Bạn Toán tìm tập xác định của hàm số bằng cách như sau:Bước 1: Ta có
y
1
(
x
-
2
)
1
2...
Đọc tiếp
Cho hàm số y = ( x - 2 ) - 1 2 Bạn Toán tìm tập xác định của hàm số bằng cách như sau:
Bước 1: Ta có y = 1 ( x - 2 ) 1 2 = 1 x - 2
Bước 2: Hàm số xác định ⇔ x - 2 > 0 ⇔ x > 2
Bước 3: Vậy tập xác định của hàm số là D = ( 2 ; + ∞ )
Lời giải trên của bạn toán đúng hay sai? Nếu sai thì sai ở bước nào?
A. Bước 3
B. Bước 1
C. Đúng
D. Bước 2
Cho các phát biểu sau(1) Đơn giản biểu thức
M
a
1
4
-
b
1
4
a
1
4
+
b
1...
Đọc tiếp
Cho các phát biểu sau
(1) Đơn giản biểu thức M = a 1 4 - b 1 4 a 1 4 + b 1 4 a 1 2 + b 1 2 ta được M = a - b
(2) Tập xác định D của hàm số y = log 2 ln 2 x - 1 là D = e ; + ∞
(3) Đạo hàm của hàm số y = log 2 ln x là y ' = 1 x ln x . ln 2
(4) Hàm số y = 10 log a x - 1 có đạo hàm tại mọi điểm thuộc tập xác định
Số các phát biểu đúng là
A. 6
B. 1
C. 3
D. 4
Cho hàm số
y
f
(
x
)
có tập xác định là
D
0
;
+
∞
,
D
0
;
+
∞
và
lim
x
→
0
+
...
Đọc tiếp
Cho hàm số y = f ( x ) có tập xác định là D = 0 ; + ∞ , D = 0 ; + ∞ và lim x → 0 + y = - ∞ ; lim x → + ∞ y = + ∞ . Mệnh đề nào sau đây đúng ?
A. Đồ thị hàm số y = f x không có tiệm cận đứng và có tiệm cận ngang.
B. Đồ thị hàm số y = f x có tiệm cận đứng và có tiệm cận ngang
C. Đồ thị hàm số y = f x có tiệm cận đứng, không có tiệm cận ngang.
D. Đồ thị hàm số y = f x không có tiệm cận đứng và không có tiệm cận ngang
Cho bài toán: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số
y
2
x
4
−
4
x
2
+
3
. Dưới đây là lời giải của học sinh:* Bước 1: Tập xác định
D
ℝ
. Đạo hàm
y
8
x
3
−
8
x
.* Bước 2: Cho
y...
Đọc tiếp
Cho bài toán: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = 2 x 4 − 4 x 2 + 3 . Dưới đây là lời giải của học sinh:
* Bước 1: Tập xác định D = ℝ . Đạo hàm y ' = 8 x 3 − 8 x .
* Bước 2: Cho y ' = 0 tìm x = 0 ; x = − 1 ; x = 1 .
* Bước 3: Tính y 0 = 3 ; y − 1 = y 1 = 1 . Vậy giá trị lớn nhất của hàm số là 3, và giá trị nhỏ nhất là 1.
Lời giải trên đúng hay sai? Nếu sai thì giải sai từ bước mấy?
A. Bước 2
B. Lời giải đúng
C. Bước 3
D. Bước 1
Cho hàm số y f(x) xác định trên khoảng (-2;-1) và có
lim
x
→
2
-
f
(
x
)
2
,
lim
x
→
1
-
f
(
x
)
-
∞
. Hỏi khẳng định nào dưới đây là khẳng định đúng? A. Đồ thị hàm số f(x) có đúng một tiệm cận ngang là đường...
Đọc tiếp
Cho hàm số y = f(x) xác định trên khoảng (-2;-1) và có lim x → 2 - f ( x ) = 2 , lim x → 1 - f ( x ) = - ∞ . Hỏi khẳng định nào dưới đây là khẳng định đúng?
A. Đồ thị hàm số f(x) có đúng một tiệm cận ngang là đường thẳng y = 2
B. Đồ thị hàm số f(x) có đúng hai tiệm cận ngang là các đường thẳng y = 2 và y = -1
C. Đồ thị hàm số f(x) có đúng một tiệm cận đứng là đường thẳng x = -1
D. Đồ thị hàm số f(x) có đúng hai tiệm cận đứng là các đường thẳng x = -2 và x = -1
Cho hàm số y f(x) có đồ thị (C) xác định trên khoảng (-2;-1) và có
lim
x
→
(
−
2
)
+
f
(
x
)
2...
Đọc tiếp
Cho hàm số y = f(x) có đồ thị (C) xác định trên khoảng (-2;-1) và có lim x → ( − 2 ) + f ( x ) = 2 , lim x → ( − 1 ) − f ( x ) = − ∞ . Khẳng định nào dưới đây đúng?
A. Đồ thị (C) có đúng hai tiệm cận ngang là đường thẳng y = 2 và y = –1
B. Đồ thị (C) có đúng một tiệm cận đứng là đường thẳng x = –1
C. Đồ thị (C) có đúng một tiệm cận ngang là đường thẳng y = 2
D. Đồ thị (C) có đúng hai tiệm cận đứng là đường thẳng x = –2 và x = –1
Cho a là một số thực dương khác 1. Có bao nhiêu mệnh đề đúng trong các mệnh đề sau: 1. Hàm số y
l
o
g
a
x
có tập xác định là D
(
0
;
+
∞
)
.
2. Hàm số y
l
o
g
a
x
là hàm đơn điệu trên khoảng
(
0
;
+
∞
)
.
3. Đồ thị hàm số y
l
o...
Đọc tiếp
Cho a là một số thực dương khác 1. Có bao nhiêu mệnh đề đúng trong các mệnh đề sau:
1. Hàm số y= l o g a x có tập xác định là D= ( 0 ; + ∞ ) .
2. Hàm số y= l o g a x là hàm đơn điệu trên khoảng ( 0 ; + ∞ ) .
3. Đồ thị hàm số y= l o g a x và đồ thị hàm số y = a x đối xứng nhau qua đường thẳng y= x.
4. Đồ thị hàm số y= l o g a x nhận Ox là một tiệm cận
A. 4
B. 1
C. 3
D. 2
Cho hàm số f(x) xác định và liên tục trên R và có đạo hàm f(x) thỏa mãn
f
(
x
)
(
1
-
x
)
(
x
+
2
)
g
(
x
)
+
2018
với
g
(
x
)
0
,
∀
x
∈
R
. Hàm số
y
f
(...
Đọc tiếp
Cho hàm số f(x) xác định và liên tục trên R và có đạo hàm f'(x) thỏa mãn f ' ( x ) = ( 1 - x ) ( x + 2 ) g ( x ) + 2018 với g ( x ) < 0 , ∀ x ∈ R . Hàm số y = f ( 1 - x ) + 2018 x + 2019 nghịch biến trên khoảng nào dưới đây?
A . ( 1 ; + ∞ ) .
B . ( 0 ; 3 ) .
C . ( - ∞ ; 3 ) .
D . ( 4 ; + ∞ ) .
Cho hàm số y f(x) xác định trên
D
−
1
;
+
∞
1
.
Dưới đây là một phần đồ thị của y f(x)Hỏi trong các mệnh đề sau, có bao nhiêu mệnh đề đúng: (I) Số điểm cực đại của hàm số trên tập xác định là 1. (II) Hàm số có cực tiểu là -2 tại x 1 (III) Hàm số đạt cực đại tại x 2 (IV) Hàm số đạt cực đại tại x -1 A. 0 B. 1 C. 2 D...
Đọc tiếp
Cho hàm số y = f(x) xác định trên D = − 1 ; + ∞ \ 1 . Dưới đây là một phần đồ thị của y = f(x)
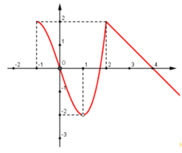
Hỏi trong các mệnh đề sau, có bao nhiêu mệnh đề đúng:
(I) Số điểm cực đại của hàm số trên tập xác định là 1.
(II) Hàm số có cực tiểu là -2 tại x = 1
(III) Hàm số đạt cực đại tại x = 2
(IV) Hàm số đạt cực đại tại x = -1
A. 0
B. 1
C. 2
D. 3

