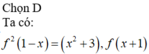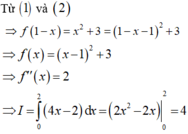Các câu hỏi tương tự
Cho hàm số f(x) có đạo hàm f(x) liên tục trên R và thỏa mãn
f
(
x
)
∈
[
-
1
;
1
]
với
∀
x
∈
(
0
;
2
)
Biết f(0) f(2) 1 Đặt
I
∫
0
2
f
(
x
)
d
x
phát bi...
Đọc tiếp
Cho hàm số f(x) có đạo hàm f'(x) liên tục trên R và thỏa mãn f ' ( x ) ∈ [ - 1 ; 1 ] với ∀ x ∈ ( 0 ; 2 ) Biết f(0) = f(2) = 1 Đặt I = ∫ 0 2 f ( x ) d x phát biểu dưới đây là ĐÚNG ?
![]()
![]()
![]()
![]()
Cho hàm số y f(x) có đạo hàm liên tục trên [1;2] thỏa mãn
∫
1
2
f
(
x
)
d
x
10
và
∫
1
2
f
(
x
)
f
(
x
)...
Đọc tiếp
Cho hàm số y = f(x) có đạo hàm liên tục trên [1;2] thỏa mãn ∫ 1 2 f ' ( x ) d x = 10 và ∫ 1 2 f ' ( x ) f ( x ) d x = ln 2 . Biết rằng f(x)>0. Tính f(2)
A. f(2) = 10
B. f(2) = -20
C. f(2) = -10
D. f(2) = 20
( Mu4-42. Cho hàm so $f(x)$ có đạo hàm trên đoạn $[0 ; 1]$ thỏa mãn $f(1)=0$ và $\int_0^1\left[f^{\prime}(x)\right]^2 d x=\int_0^1(x+1) e^x f(x) d x=\frac{e^2-1}{4}$. Tinh tich phân $I=\int_{0}^1 f(x) d x$.
A. $I=2-e$.
B. $I=\frac{e}{2}$.
C. $l=e-2$.
D. $1=\frac{e-1}{2}$
Cho hàm số y f(x) liên tục và có đạo hàm trên R thỏa mãn f(2) -2;
∫
0
2
f
(
x
)
d
x
1
Tính tích phân
I
∫
0
4
f
(
x
)
d
x
A. I -10 B. I -5 C. I 0 D. I -18
Đọc tiếp
Cho hàm số y = f(x) liên tục và có đạo hàm trên R thỏa mãn f(2) = -2; ∫ 0 2 f ( x ) d x = 1 Tính tích phân I = ∫ 0 4 f ' ( x ) d x
A. I = -10
B. I = -5
C. I = 0
D. I = -18
Cho hàm số f(x) có đạo hàm dương, liên tục trên đoạn [0;1] thỏa mãn điều kiện f(0)1 và
3
∫
0
1
f
(
x
)
.
f
(
x
)
2
+...
Đọc tiếp
Cho hàm số f(x) có đạo hàm dương, liên tục trên đoạn [0;1] thỏa mãn điều kiện f(0)=1 và 3 ∫ 0 1 f ' ( x ) . f ( x ) 2 + 1 9 d x ≤ 2 ∫ 0 1 f ' ( x ) . f ( x ) d x Tính ∫ 0 1 f ( x ) 3 d x
A. 3/2
B. 5/4
C. 5/6
D. 7/6
Cho hàm số liên tục trên khoảng (a;b) và
x
0
∈
(
a
;
b
)
.
Có bao nhiêu mệnh đề đúng trong các mệnh đề sau?(1) Hàm số đạt cực trị tại điểm
x
0
khi và chỉ khi
f
(
x
0
)
0
.
(2) Nếu hàm số
y
f
(
x
)
có đạo hàm và có đạo...
Đọc tiếp
Cho hàm số liên tục trên khoảng (a;b) và x 0 ∈ ( a ; b ) . Có bao nhiêu mệnh đề đúng trong các mệnh đề sau?
(1) Hàm số đạt cực trị tại điểm x 0 khi và chỉ khi f ' ( x 0 ) = 0 .
(2) Nếu hàm số y = f ( x ) có đạo hàm và có đạo hàm cấp hai tại điểm x 0 thỏa mãn điều kiện f ' ( x 0 ) = f ' ' ( x 0 ) = 0 thì điểm x 0 không phải là điểm cực trị của hàm số y = f ( x ) .
(3) Nếu f'(x) đổi dấu khi x qua điểm x 0 thì điểm x 0 là điểm cực tiểu của hàm số y = f ( x ) .
(4) Nếu hàm số y = f ( x ) có đạo hàm và có đạo hàm cấp hai tại điểm x 0 thỏa mãn điều kiện f ' ( x 0 ) = 0 , f ' ' ( x 0 ) > 0 thì điểm x 0 là điểm cực tiểu của hàm số y = f ( x ) .
A. 1
B. 2
C. 0
D. 3
Cho hàm số y f(x) liên tục và có đạo hàm trên R thỏa mãn f(2) -2;
∫
0
2
f
(
x
)
d
x
1
Tính tích phân
∫
0
4
f
(
x
)
d
x
A. I -10 B. I -5 C. I 0 D. I -18
Đọc tiếp
Cho hàm số y =f(x) liên tục và có đạo hàm trên R thỏa mãn f(2) = -2; ∫ 0 2 f ( x ) d x = 1 Tính tích phân ∫ 0 4 f ' ( x ) d x
A. I = -10
B. I = -5
C. I = 0
D. I = -18
Cho hàm số f(x) có đạo hàm không âm trên [0;1] thỏa mãn
[
f
(
x
)
]
4
.
[
f
(
x
)
]
2
(
x
2
+
1
)
1...
Đọc tiếp
Cho hàm số f(x) có đạo hàm không âm trên [0;1] thỏa mãn [ f ( x ) ] 4 . [ f ' ( x ) ] 2 ( x 2 + 1 ) = 1 + f 3 ( x ) và f(x)>0 biết f(0) = 2 Hãy chọn khẳng định đúng trong các khẳng định sau:
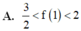
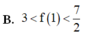
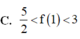
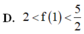
Cho hàm số f(x) có đạo hàm trên R thỏa mãn f(x)-2018f(x)
2018
x
2017
e
2018
x
với mọi
x
∈
ℝ
, f(0)2018. Tính f(1)
Đọc tiếp
Cho hàm số f(x) có đạo hàm trên R thỏa mãn f'(x)-2018f(x)= 2018 x 2017 e 2018 x với mọi x ∈ ℝ , f(0)=2018. Tính f(1)
![]()
![]()
![]()
![]()