Question

Hai gương phẳng có mặt phản xạ quay vào nhau hợp nhau tạo góc nhọn . chiếu 1 tia sáng SI đến gương thứ nhất phản xạ theo gương IJ đến gương thứ 2 rồi phản xạ tiếp theo gương JR. Tìm góc beta hợp bởi 2 tia SI và JR

Answer 1

de

Answer 2

Bạn viết đùng đề không vậy bạn ?

Answer 3

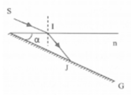
β=2α (α là góc tạo bởi 2 gương)

Answer 4

gọi K là giao điểm củaSI và JR

pháp tuyến JF cắt SI tại F, và cắt pháp tuyến IE tại M, kẻ OM( O là giao điểm của 2 mặt gương)

ta có : JKI=180-(KJF+JFK)=180-( KJF+ FIM+ IMF)=180-2\(\alpha\)(vì tứ giác IOJM là tứ giác nội tiếp=>IOJ+JMI=180, mà JMI+IMF=180=> IOJ=IMF=\(\alpha\), cũng vì tứ giác IOJM nội tiếp=>IOM=IJM, JIM=MOJ=> FIM+ KIF=\(\alpha\)).

Answer 5

theo mình nghĩ thì như vậy