Tọa độ giao điểm của 2 đường thẳng đã cho nếu có thì thỏa mãn hệ phươngtrình sau:
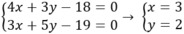
Chọn B.
Tọa độ giao điểm của 2 đường thẳng đã cho nếu có thì thỏa mãn hệ phươngtrình sau:
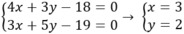
Chọn B.
Bài 1: Trong mặt phẳng với hệ toạ độ Đềcác vuông góc Oxy, cho đường thẳng (∆): 2x+y+3=0 và hai điểm A(-5;1), B(-2;4) 1. Viết phương trình đường tròn C đi qua A,B và có tâm I∈ (∆). 2. Viết phương trình đường tiếp tuyến tại A với đường tròn C. 3. Viết phương trình các tiếp tuyến với (C), biết tiếp tuyến đi qua D(1;2). Tìm toạ độ tiếp điểm. Bài 2: Trong mặt phẳng với hệ toạ độ Oxy cho điểm I(-2;1) và đường thẳng d: 3x-4y=0 a. Viết phương trình đường tròn (C) có tâm I và tiếp xúc với đường thẳng d. b. Viết phương trình tập hợp các điểm mà qua các điểm đó vẽ được hai tiếp tuyến đến (C) sao cho hai tiếp tuyến vuông góc với nhau.
Tìm khoảng cách từ một điểm đến đường thẳng trong các trường hợp sau:
a, A(3; 5) và Δ : 4x + 3y +1 = 0
b, B(1; -2) và d: 3x – 4y -26 = 0
c, C(1; 2) và m: 3x + 4y -11 = 0
Tìm Parabol y = ax2 - 4x + c, biết rằng Parabol :
Đi qua hai điểm A(1; -2) và B(2; 3).
Có đỉnh I(-2; -2).
Có hoành độ đỉnh là -3 và đi qua điểm P(-2; 1).
Có trục đối xứng là đường thẳng x = 2 và cắt trục hoành tại điểm (3; 0).
Trong một mặt phẳng toạ độ xOy cho tam giác AC vuông tại A có đường cao AH: x- 3y-16=0 cắt đường phân giác BD tại K( \(D\in AC\)) , đường thẳng đi qua K song song với AC và cắt cạnh huyền BC tại E ( 3;-7), biết điểm D thuộc đường thẳng\(\Delta:x-y-12=0\) và xA>3. Viết phương trình các cạnh của tam giác ABC
Cho tam giác ABC có đỉnh A(-1;-3) và hai đường cao xuất phát từ B và C lần lượt là ( BH ) :5x + 3y - 25 = 0
( CK ) : 3x + 8y - 12 = 0 . Viết phương trình cạnh BC và toạ độ điểm B và C của tam giác.
Trong mặt phẳng tọa độ Oxy , Cho hai điểm A(3;5), B(1;-7) và đường thẳng d:4x+3y-5=0. 1) viết phương trình đường tròn(c) có tâm thuộc trục Oy và đi qua hai điểm A,B 2) viết phương trình tiếp tuyến của (C) biết tiếp tuyến song song với đường thẳng d 3) tìm tọa độ điểm M thuộc đường thẳng d Sao cho |3MA+2MB+MC| Đạt giá trị nhỏ nhất
Cho A( -2; 5) và B(2;3). Đường thẳng d: x- 4y+ 4= 0 cắt AB tại M. Toạ độ điểm M là:
A. (8;3)
B. (0; 1)
C. (4; 2)
D. (4; -2)
Câu 1. Cho tam giác ABC với A(1; 2), B(−2; 5) và C(0; 1). Gọi H, K lần lượt là chân đường cao kẻ từ
các đỉnh A, B. Hãy chỉ ra một véc-tơ pháp tuyến của mỗi đường thằng AH, BK.
Câu 2. Cho hai đường thẳng d1 : −3x + y − 2 = 0 và d2 : 2x − 3 = 0.
a) Hãy chỉ ra một VTPT của d1, d2.
b) Trong các điểm A(2; 0), B(−1; −1), C(\(\frac{3}{2}\); 1), D(\(\frac{3}{2}\); \(\frac{13}{2}\)) điểm nào thuộc d1, điểm nào thuộc d2?
Câu 3. Viết phương trình tổng quát của đường thẳng d biết
a) d đi qua điểm A(−2; 5) và có VTPT −→n = (−1; 2).
b) d đi qua điểm A(−5; 2) và vuông góc với đường thẳng BC biết tọa độ điểm B(1; 1) và
C(2; 3).
c) d đi qua điểm A(−1; 1) và song song với đường thẳng d': −4x − y + 2 = 0.
Đường thẳng y=3 cắt trục 0y tại điểm có tọa độ là A (0:-3) B (3:0) c(1:3) d(0:3)