Vì L và M đối xứng qua đường thẳng xy nên xy là đường thẳng đi qua trung điểm và vuông góc với ML.
Nên đường thẳng xy là trung trực của ML.
I ∈ xy ⇒ IM = IL (theo định lý 1).
Nên IM + IN = IL + IN
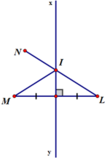
- TH1: Nếu I, L, N thẳng hàng
⇒ IL + IN = LN (vì N và L nằm khác phía so với đường thẳng xy và I nằm trên xy).
⇒ IM + IN = LN
- TH2: Nếu I không là giao điểm của LN và xy thì ba điểm I, L, N không thẳng hàng
Áp dụng bất đẳng thức tam giác vào Δ INL ta được: IL + IN > LN
mà IM = IL (cmt)
⇒ IL + IN > LN (bất đẳng thức tam giác)
⇒ IM + IN > LN
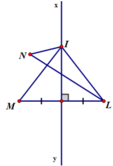
Vậy với mọi vị trí của I trên xy thì IM + IN ≥ LN

