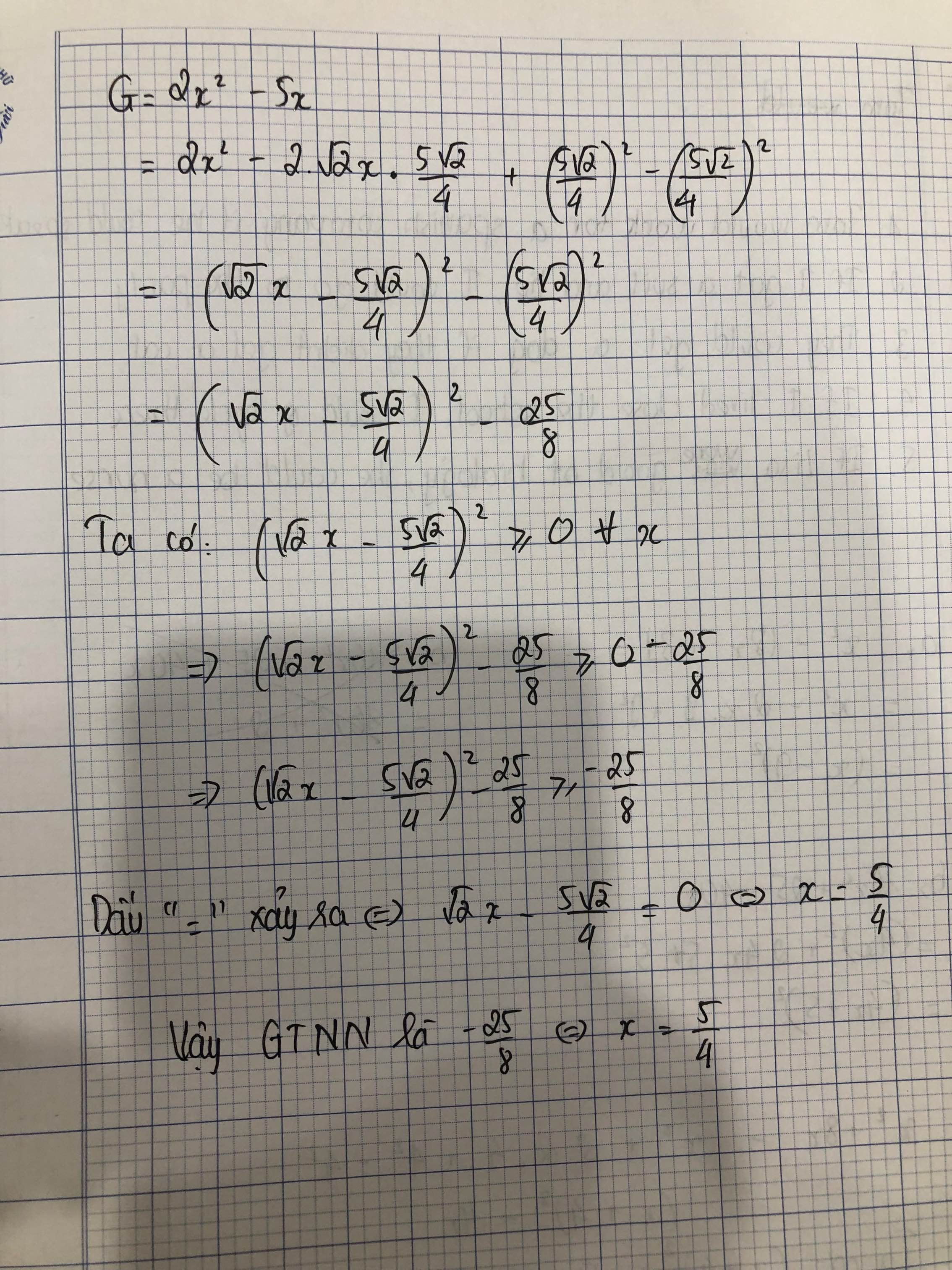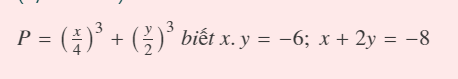\(H=x^2+8x\\ =x^2+8x+16-16\\ =\left(x+4\right)^2-16\ge-16\)
Dấu "=" xảy ra \(\Leftrightarrow x+4=0\Leftrightarrow x=-4\)
\(G=2x^2-5x\\ =2\left(x^2-\dfrac{5}{2}x\right)\\ =2\left(x^2-2.\dfrac{5}{4}x+\dfrac{25}{16}-\dfrac{25}{16}\right)\\ =2\left(x-\dfrac{5}{4}\right)^2-\dfrac{25}{8}\ge-\dfrac{25}{8}\)
Dấu "=" xảy ra \(\Leftrightarrow x-\dfrac{5}{4}=0\Leftrightarrow x=\dfrac{5}{4}\)
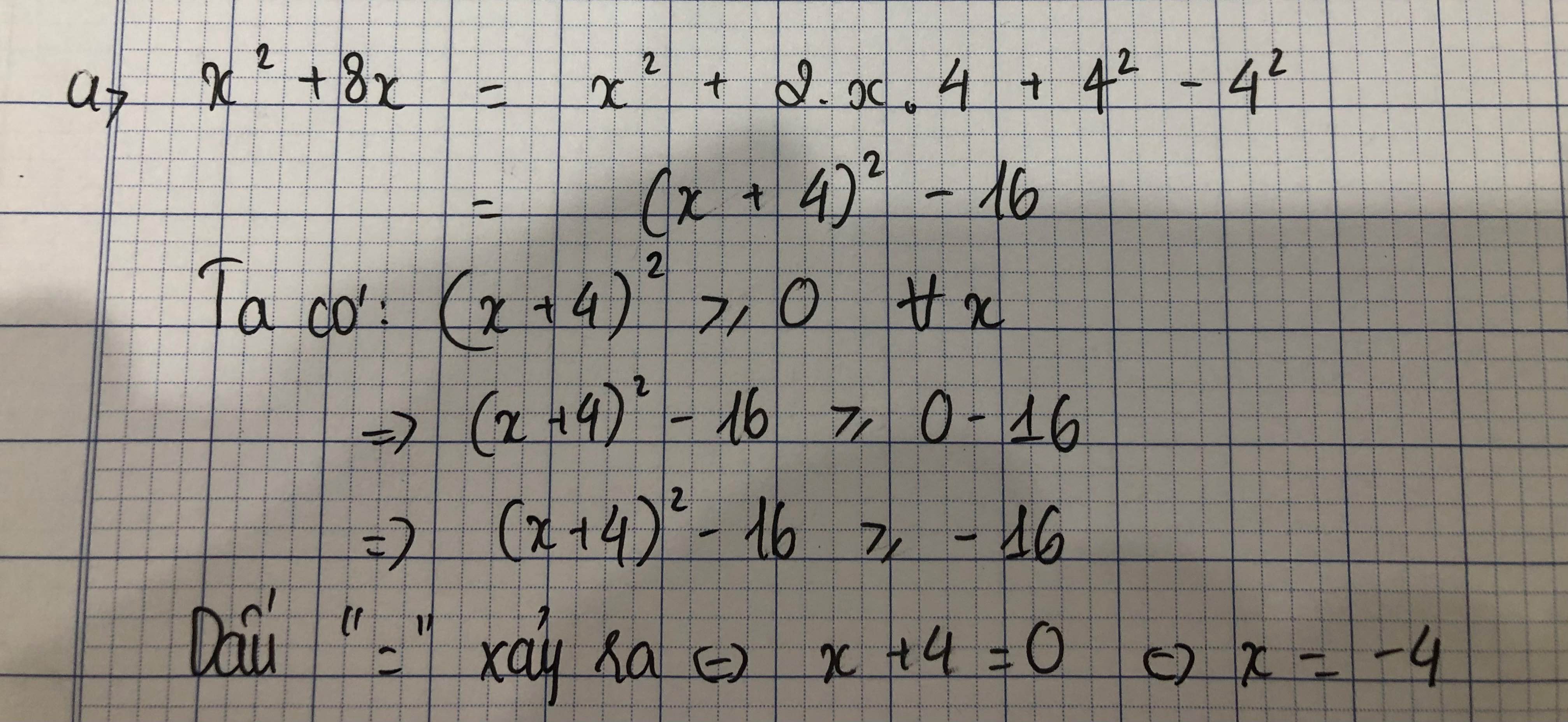
vậy GTNN của phương trình trên là: -16 <=> x = -4