Đáp án D
x = 0 ⇒ y = − 3 ⇒ B 0 ; − 3
y = 0 ⇒ x = 3 2 ⇒ A 3 2 ; 0
S O A B = 1 2 . O A . O B = 1 2 .3. 3 2 = 9 4 .
Đáp án D
x = 0 ⇒ y = − 3 ⇒ B 0 ; − 3
y = 0 ⇒ x = 3 2 ⇒ A 3 2 ; 0
S O A B = 1 2 . O A . O B = 1 2 .3. 3 2 = 9 4 .
Biết điểm A có hoành độ lớn hơn – 4 là giao điểm của đường thẳng y = x + 7 với đồ thị (C) của hàm số y = 2 x - 1 x + 1 . Tiếp tuyến của đồ thì (C) tại điểm A cắt hai trục độ Ox, Oy lần lượt tịa E, F. Khi đó tam giác OEF (O là gốc tạo độ) có diện tích bằng:
A. 33 2
B. 121 2
C. 121 3
D. 121 6
Biết đồ thị hàm số y = x - 2 x + 1 các trục Ox,Oy lần lượt tại hai điểm phân biệt A, B. Tính diện tích S của tam giác OAB
A. S=1
B. S = 1 2
C. S = 2
D. S = 4
Gọi A;B;C lần lượt là các điểm cực trị của đồ thị hàm số y = x 4 − 2 x 2 + 3 . Diện tích của tam giác ABC bằng?
A. 2
B. 2 2
C. 1
D. 2
Cho đồ thị hàm số C : y = 1 x ; điểm M có hoành độ x M = 2 − 3 thuộc (C). Biết tiếp tuyến của (C) tại M lần lượt cắt Ox, Oy tại A, B. Tính diện tích tam giác OAB.
A. S Δ O A B = 1.
B. S Δ O A B = 4.
C. S Δ O A B = 2.
D. S Δ O A B = 2 + 3 .
Tìm giá trị của tham số m để đồ thị hàm số y=x4-2(m+1)x2+2m+3 có 3 điểm cực trị A,B,C là ba đỉnh của một tam giác, trục hoành chia tam gíac ABC thành một tam giác và một hình thang sao cho tỉ số diện tích tam giác nhỏ được chia ra và diện tích tam giác ABC bằng 4/9
![]()
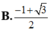
![]()
![]()
Cho hàm số y = x 3 - 3 x 2 + m 1 . Tìm m để tiếp tuyến của đồ thị (1) tại điểm có hoành độ bằng 1 cắt các trục Ox, Oy lần lượt tại các điểm A, B mà diện tích tam giác OAB bằng 3 2
A. m = 3 h o ặ c m = - 1
B. m = 2
C. m = - 4 h o ặ c m = 2
D. m = 3
Cho hàm số y = x 3 − 3 x 2 + m (1). Tìm m để tiếp tuyến của đồ thị (1) tại điểm có hoành độ bằng 1 cắt các trục Ox, Oy lần lượt tại các điểm A, B mà diện tích tam giác OAB bằng 3 2 .
A. m = 2
B. m = 3 hoặc m = -1
C. m = 4 hoặc m = 2
D. m = 3
Biết đồ thị hàm số y = 2 x − 1 x + 3 cắt trục Ox, Oy lần lượt tại hai điểm phân biệt A, B. Tính diện tích S của tam giác OAB.
A. S = 1 12 .
B. S = 1 6 .
C. S = 3.
D. S = 6.
Cho hàm số y = a x 4 + b x 2 + c có đồ thị (C), biết rằng (C) đi qua điểm A(-1;0) tiếp tuyến d tại A của (C) cắt (C) tại hai điểm có hoành độ lần lượt là 0 và 2, diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x=0; x=2 có diện tích bằng 28 5 (phần gạch chéo trong hình vẽ). Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x=-1; x=0 có diện tích bằng:

A. 2 5
B. 1 9
C. 2 9
D. 1 5