Đáp án A
Phương trình ![]()
![]()
hoặc 4 nghiệm là ![]()
Đáp án A
Phương trình ![]()
![]()
hoặc 4 nghiệm là ![]()
Trong không gian OxyzOxyz cho hai điểm A(2;4;3)A(2;4;3) và B(2;7;1)B(2;7;1). Trong các phương trình dưới đây, phương trình nào là phương trình tham số của đường thẳng ABAB? (với t\in \Rt∈R)
A,\left\{{}\begin{matrix}x=2+2t\\y=7+4t\\z=1+3t\end{matrix}\right.⎩⎪⎨⎪⎧x=2+2ty=7+4tz=1+3t
B,\left\{{}\begin{matrix}x=4\\y=3+3t\\z=2-2t\end{matrix}\right.⎩⎪⎨⎪⎧x=4y=3+3tz=2−2t
c,\left\{{}\begin{matrix}x=2\\y=4-3t\\z=3+2t\end{matrix}\right.⎩⎪⎨⎪⎧x=2y=4−3tz=3+2t
d,\left\{{}\begin{matrix}x=2+2t\\y=4+7t\\z=3+t\end{matrix}\right.⎩⎪⎨⎪⎧x=2+2ty=4+7tz=3+t
Gọi tổng cần tìm là T. Tính tổng bình phương các nghiệm của phương trình: z + 1 i z + 1 i 2 . . . . z + 1 i 15 = 0
A. T = 0
B. T = 4
C. T = 15i
D. T = 15 2
Tìm nghiệm của phương trình: ( z + 3 - i)2 - 6( z + 3 - i) + 13 = 0
A. z = 3i; z = 1 - 2i
B. z = - i; z = 3i + 4
C. z = 3i + 4; z = 3i
D. z = 3i; z = -i
Cho (d): x = t; y = 3t – 2, z = 4t +6 và △ : x - 5 1 = y + 1 - 4 = z - 20 1 . Chọn mệnh đề đúng .
![]()
B. d ⊥ ∆ d c 3 4 t ∆
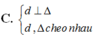
![]()
Số phức z=a+bi, a,b thuộc R là nghiệm của phương trình ( z - 1 ) ( 1 + i z z - 1 z = i . Tổng T=a^2+b^2 bằng
A. ![]() .
.
B. ![]() .
.
C.![]()
D. ![]() .
.
Phương trình: ( z + 3 - i ) 2 - 6(z + 3 - i) + 13 = 0 có 2 nghiệm phân biệt. Khẳng định nào sau đây là đúng?
A. Trong 2 nghiệm có một nghiệm bằng 0.
B. Cả 2 nghiệm đều là số thực.
C. Cả 2 nghiệm đều là số thuần ảo.
D. Trong 2 nghiệm có 1 nghiệm là số thực, 1 nghiệm là số thuần ảo.
Gọi z1; z2; z3; z4 là bốn nghiệm của phương trình ( z - 1 )( z + 2) ( z2 - 2z + 2) = 0 trên tập số phức, tính tổng: 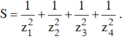
A. 2/5
B. 3/5
C. 5/4
D. 6/7
Cho a , b , c , x , y , z là các số thực thay đổi thỏa mãn ( x + 1 ) 2 + ( y + 1 ) 2 + ( z - 2 ) 2 = 4 và a + b + c = 6 . Tính giá trị nhỏ nhất của P = ( x - a ) 2 + ( y - b ) 2 + ( z - c ) 2 . .
![]()
![]()
![]()
Tìm số phức Z, biết Z là nghiệm của phương trình: ( 2 i - 1 ) Z 2 - 2 i Z ¯ + ( 6 + 4 i ) = 0
A. Z = -i
B. Z = 1-i
C. Z = 1+i
D. Z = i
Gọi z 1 ; z 2 là hai nghiệm phức của phương trình 3 z 2 - z + 2 = 0 . Tính giá trị biểu thức T = z 1 2 + z 2 2 .
A. T = 2 3
B. T = 8 3
C. T = 4 3
D. T = - 11 9