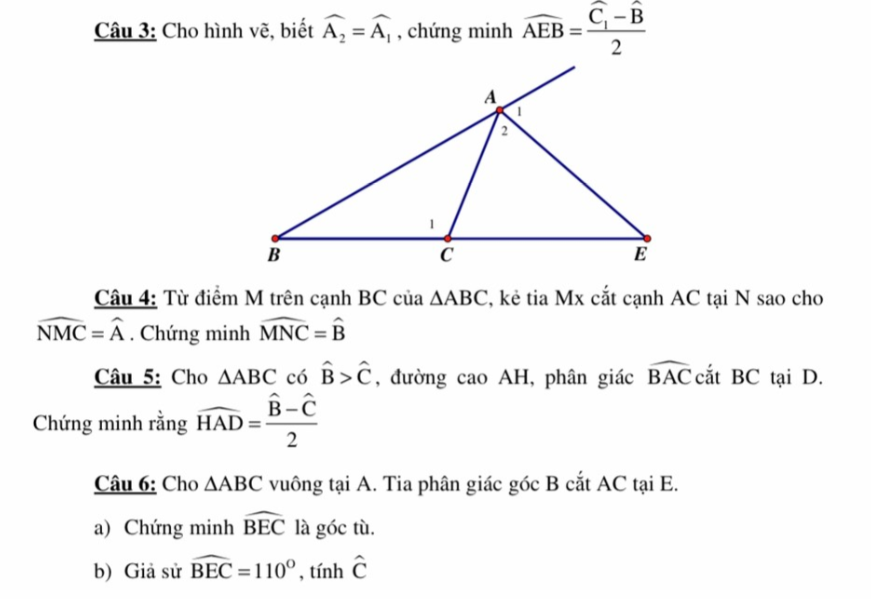
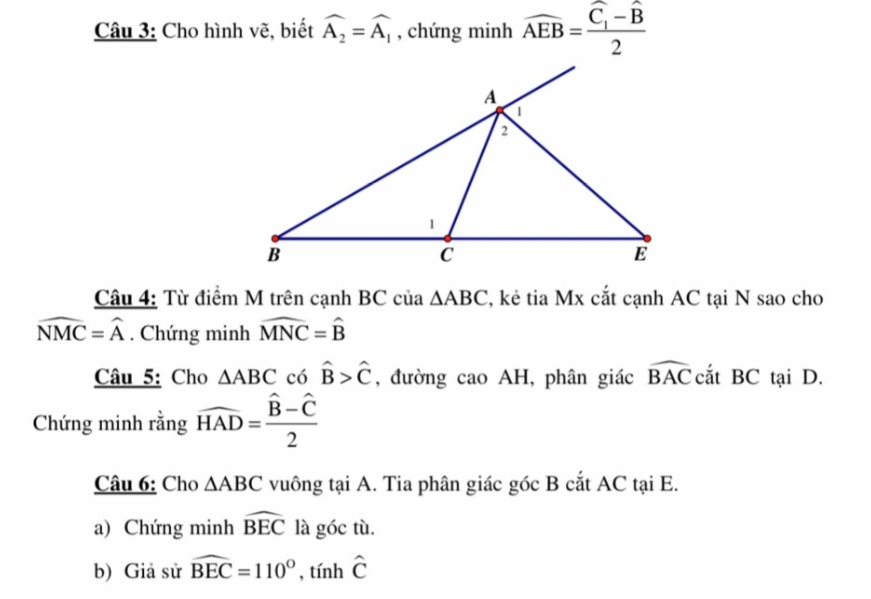
Câu 3:
Theo tính chất góc ngoài:
\(\widehat{AEB}=\widehat{C_1}-\widehat{A_2}=\widehat{C_1}-\widehat{A_1}=\widehat{C_1}-\widehat{B}-\widehat{AEB}\\ \Rightarrow2\widehat{AEB}=\widehat{C_1}-\widehat{B}\\ \Rightarrow\widehat{AEB}=\dfrac{\widehat{C_1}-\widehat{B}}{2}\)
Bài 4:
Vì \(\left\{{}\begin{matrix}\widehat{MNC}+\widehat{NMC}+\widehat{C}=180^0\\\widehat{A}+\widehat{B}+\widehat{C}=180^0\end{matrix}\right.\) và \(\widehat{NMC}=\widehat{A}\)
Do đó \(\widehat{MNC}=\widehat{B}\)
Bài 5:
\(\widehat{HAD}=\widehat{BAD}-\widehat{BAH}=\dfrac{\widehat{BAC}}{2}-\left(90^0-\widehat{B}\right)=\dfrac{\widehat{BAC}}{2}-90^0+\widehat{B}=\dfrac{\widehat{BAC}}{2}-90^0+180^0-\widehat{BAC}-\widehat{C}=\dfrac{\widehat{BAC}+180^0-2\widehat{BAC}-2\widehat{C}}{2}=\dfrac{\left(180^0-\widehat{BAC}\right)-2\widehat{C}}{2}=\dfrac{\widehat{B}+\widehat{C}-2\widehat{C}}{2}=\dfrac{\widehat{B}-\widehat{C}}{2}\)
Bài 6:
a, Theo tc góc ngoài: \(\widehat{BEC}=\widehat{A}+\widehat{BCE}=90^0+\widehat{BCE}>90^0\left(đpcm\right)\)
b, \(\widehat{C}=180^0-\widehat{BEC}-\widehat{CBE}=180^0-110^0-\widehat{CBE}=70^0-\widehat{CBE}\)
Mà BE là p/g nên \(\widehat{C}=70^0-\dfrac{\widehat{ABC}}{2}=70^0-\dfrac{90^0-\widehat{C}}{2}=\dfrac{140^0-90^0+\widehat{C}}{2}\)
\(\Rightarrow2\widehat{C}=30^0+\widehat{C}\\ \Rightarrow\widehat{C}=30^0\)



 giúp mình với ạ,mình cần gấp lắm
giúp mình với ạ,mình cần gấp lắm
 Các bạn giải cả 3 bài này giúp mình với, mình đang gấp nhớ vẽ hình lun ạ !!! Cảm ơn
Các bạn giải cả 3 bài này giúp mình với, mình đang gấp nhớ vẽ hình lun ạ !!! Cảm ơn