Chọn đáp án C
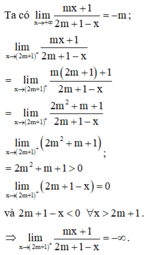
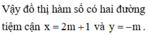
Hai đường tiệm cận tạo với hai trục tọa độ một hình chữ nhật có diện tích bằng 3 suy ra
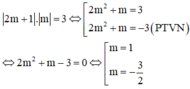
Chọn đáp án C
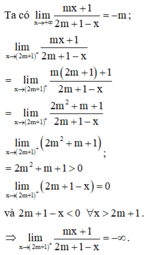
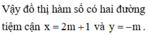
Hai đường tiệm cận tạo với hai trục tọa độ một hình chữ nhật có diện tích bằng 3 suy ra
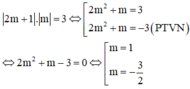
Tìm tất cả các giá trị của tham số m sao cho đồ thị C m của hàm số y = 2 x + m x m + 1 có tiệm cận đứng, tiệm cận ngang và các tiệm cận cùng với hai trục tọa độ tạo thành một hình chữ nhật có diện tích bằng 8
A. m = ± 1 4
B. m = ± 1 2
C. m = ± 1 8
D. không có m thỏa mãn
Với giá trị nào của m thì tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = 3 x + 2 m m x + 1 cùng với 2 trục tọa độ tạo thành 1 hình chữ nhật có diện tích là 12?
A. m = 2
B. m = ± 2
C. m = ± 1 2
D. m = − 1
Cho hàm số y = x - 1 x + 2 , gọi d là tiếp tuyến với đồ thị hàm số tại điểm có hoành độ bằng m - 2. Biết đường thẳng d cắt tiệm cận đứng của đồ thị hàm số tại điểm A(x1;y1) và cắt tiệm cận ngang của đồ thị hàm số tại điểm B(x2;y2). Gọi S là tập hợp các số m sao cho x2 + y1 = -5. Tính tổng bình phương các phần tử của S
A. 4
B. 0
C. 10
D. 9
Cho hàm số y = 2 x - 1 2 x - 2 có đồ thị (C). Gọi M x 0 ; y 0 (với x 0 > 1 ) là điểm thuộc (C), biết tiếp tuyến của (C) tại M cắt tiệm cận đứng và tiệm cận ngang lần lượt tại A và B sao cho S ∆ O I B = 8 S ∆ O I A (trong đó O là gốc tọa độ, I là giao điểm hai tiệm cận). Giá trị của S = x 0 + 4 y 0 bằng
A. 8
B. 2
C. 17 4
D. 23 4
Cho hàm số y = 2 x − 2 x − 2 có đồ thị là (C). M là điểm thuộc (C) sao cho tiếp tuyến của (C) tại M cắt hai đường tiệm cận của (C) tại hai điểm A, B thỏa mãn A B = 2 5 . Gọi S là tổng các hoành độ của tất cả các điểm M thỏa mãn bài toán. Giá trị của S bằng:
A. 8
B. 5
C. 7
D. 6
Biết rằng hai đường tiệm cận của đồ thị hàm số y = 2 x + 1 x - m (m là tham số thực) tạo với hai trục tọa độ một hình chữ nhật có diện tích bằng 2. Giá trị của m bằng bao nhiêu?
A. m = ± 1
B. m = ± 2
C. m = 2
D. m = 1
Biết rằng hai đường tiệm cận của đồ thị hàm số y = 2 x + 1 x − m (m là tham số thực) tạo với hai trục tọa độ một hình chữ nhật có diện tích bằng 2. Giá trị của m bằng bao nhiêu ?
A. m = ± 1
B. m = ± 2
C. m = 2
D. m = 1
Gọi S là tập hợp tất cả các giá trị của tham số thực m sao cho đồ thị hàm số f x = x x 3 + m x + 1 - x 4 + x + 1 3 + m 2 x nhận trục tung làm tiệm cận đứng. Khi đó tích các phần tử của S bằng
A. -1/2
B. 1/2
C. 1/3
D. -1/3
Biết rằng đồ thị hàm y = ( m - 2 n - 3 ) x + 5 x - m - n số nhận hai trục tọa độ làm hai đường tiệm cận. Tính tổng S = m 2 + n 2 - 2 .
A.S=2
B.S=0
C.S=-1
D.S=1