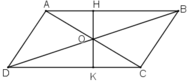
Gọi OH, OK lần lượt là chiều cao của tam giác AOB và tam giác DOC.
Ta có: OK ⊥ CD, CD // AB ⇒ OK ⊥ AB ⇒ O, H, K thẳng hàng.
Do đó:
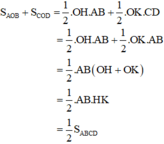
Mà SABCD = SAOB + SBOC + SCOD + SDOA

Do đó SAOB + SCOD = SBOC + SDOA.

Gọi OH, OK lần lượt là chiều cao của tam giác AOB và tam giác DOC.
Ta có: OK ⊥ CD, CD // AB ⇒ OK ⊥ AB ⇒ O, H, K thẳng hàng.
Do đó:
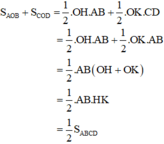
Mà SABCD = SAOB + SBOC + SCOD + SDOA

Do đó SAOB + SCOD = SBOC + SDOA.
Gọi O là điểm nằm trong hình bình hành ABCD. Chứng minh rằng tổng diện tích của hai tam giác ABO và CDO bằng tổng diện tích của hai tam giác BCO và DAO
Gọi O là điểm nằm trong hình bình hành ABCD.Chứng minh rằng tổng diện tích của hai tam giác ABO và CDO bằng tổng diện tích của hai tam giác BCO và DAO
Cho tứ giác ABCD có hai đường chéo cắt nhau tại O. Biết rằng diện tích của các tam giác ABO, BCO, CDO và DAO là những số nguyên. Chứng minh tích các số đo diện tích của các tam giác đó là một số chính phương.
Chứng minh rằng nếu O là một điểm bất kì nằm trong tứ giác ABCD sao cho diện tích các \(\Delta ABO;BCO;CDO;DAO\)
bằng nhau thì O phải thuộc một trong hai đường chéo AC và BD
GÍUP MÌNH Với!!
1. Tính diện tích một hình thang vuông, biết hai đáy có độ dài 6cm và 9cm, góc tạo bởi cạnh bên và đáy lớn có số đo bằng 45o
2. Cho hình thang ABCD có độ dài hai đáy AB = 5cm, CD = 15cm, độ dài hai đường chéo AC = 16cm, BD = 12cm. Từ A vẽ đường thẳng song song với BD, cắt CD tại E
a) Chứng minh tam giác ACE là tam giác vuông
b) Tính diện tích hình thang ABCD
3. Gọi O là điểm nằm trong hình bình hành ABCD . Chứng minh: SABO + SCDO = SBCO + SDAO
5) Trên cạnh AB và CD của hình bình hành ABCD lần lượt lấy hai điểm M và N sao cho AM = CN, P là điểm trên AD, các đường thẳng MN, BP, CP chia hình bình hành thành ba tam giác và ba tứ giác. Chứng minh rằng trong đó diện tích một tam giác bằng tổng diện tích hai tam giác còn lại, và diện tích một tứ giác bằng tổng diện tích hai tứ giác còn lại.
hình bình hành abcd với o là giao điểm hai đường chéo. cmr các giao điểm của các đường phân giác của các tam giác abo, bco, cdo, dao là các đỉnh của 1 hình thoi.
CHO TỨ GIÁC LỒI ABCD
A) CM NẾU MỖI ĐƯỜNG CHÉO PHÂN TỨ GIÁC THÀNH 2 TAM GIÁC CÓ DIỆN TÍCH BẰNG NHAU THÌ ABCD LÀ HÌNH BÌNH HÀNH
B) CM NẾU O LÀ 1 ĐIỂM TRONG TỨ GIÁC SAO CHO SABO=SBCO=SCDO=SDAO THÌ O THUỘC AC HAY O THUỘC BD
Cho tứ giác lồi ABCD
a/ C/m nếu mỗi đường chéo phân tứ giác thành 2 tam giác có diện tích bằng nhau thì ABCD là hình bình hành .
b/ C/m nếu O là 1 điểm trong tứ giác sao cho SABO=SBCO=SCDO=SDAO thì O thuộc AC hay O thuộc BD