Các câu hỏi tương tự
Cho hình trụ có bán kính đáy bằng a và chiều cao bằng h. Tính thể tích V của khối lăng trụ tam giác đều nội tiếp hình trụ đã cho. A.
V
3
a
2
h
4
B.
V
3
3
a
2
h
4...
Đọc tiếp
Cho hình trụ có bán kính đáy bằng a và chiều cao bằng h. Tính thể tích V của khối lăng trụ tam giác đều nội tiếp hình trụ đã cho.
A. V = 3 a 2 h 4
B. V = 3 3 a 2 h 4
C. V = π 3 h 2 + 4 a 2 3 h 2 4 + a 2 3
D. V = 3 3 π a 2 h 4
Một hình trụ có bán kính r và chiều cao h r√3.a) Tính diện tích xung quanh và diện tích toàn phần của hình trụ.b) TÍnh thể tích khối trụ tạo nên bởi hình trụ đã cho.c) Cho hai điểm A và B lần lượt nằm trên hai đường tròn đáy sao cho góc giữa đường thẳng AB và trục của hình trụ bằng 300. TÍnh khoảng cách giữa đường thẳng AB và trục của hình trụ
Đọc tiếp
Một hình trụ có bán kính r và chiều cao h = r√3.
a) Tính diện tích xung quanh và diện tích toàn phần của hình trụ.
b) TÍnh thể tích khối trụ tạo nên bởi hình trụ đã cho.
c) Cho hai điểm A và B lần lượt nằm trên hai đường tròn đáy sao cho góc giữa đường thẳng AB và trục của hình trụ bằng 300. TÍnh khoảng cách giữa đường thẳng AB và trục của hình trụ
Một khúc gỗ có dạng khối nón có bán kính đáy r 30 km, chiều cao h 120 km. Anh thợ mộc chế tác khúc gỗ đó thành một khúc gỗ có dạng khối trụ như hình vẽ. Gọi V là thể tích lớn nhất của khúc gỗ dạng khối trụ có thể chế tác được. Tính V A.
V
0
,
16
m
3
B.
V
0
,
024
m
3
C.
V...
Đọc tiếp
Một khúc gỗ có dạng khối nón có bán kính đáy r= 30 km, chiều cao h= 120 km. Anh thợ mộc chế tác khúc gỗ đó thành một khúc gỗ có dạng khối trụ như hình vẽ. Gọi V là thể tích lớn nhất của khúc gỗ dạng khối trụ có thể chế tác được. Tính V
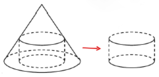
A. V = 0 , 16 m 3
B. V = 0 , 024 m 3
C. V = 0 , 027 m 3
D. V = 0 , 016 m 3
Một khúc gỗ có dạng khối nón có bán kính đáy r 30cm, chiều cao h 120cm. Anh thợ mộc chế tác khúc gỗ đó thành một khúc gỗ có dạng khối trụ như hình vẽ. Gọi V là thể tích lớn nhất của khúc gỗ dạng khối trụ có thể chế tác được. Tính V. A.
V
0
,
16
π
m
3
. B.
V
0
,
024
π...
Đọc tiếp
Một khúc gỗ có dạng khối nón có bán kính đáy r = 30cm, chiều cao h = 120cm. Anh thợ mộc chế tác khúc gỗ đó thành một khúc gỗ có dạng khối trụ như hình vẽ.
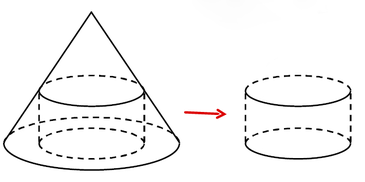
Gọi V là thể tích lớn nhất của khúc gỗ dạng khối trụ có thể chế tác được. Tính V.
A. V = 0 , 16 π m 3 .
B. V = 0 , 024 π m 3 .
C. V = 0 , 36 π m 3 .
D. V = 0 , 016 π m 3 .
Để định vị một trụ điện, người ta cần đúc một khối bê tông có chiều cao
h
1
,
5
m
gồm:- Phần dưới có dạng hình trụ bán kính đáy
R
1
m
và có chiều cao bằng
1
3
h
;- Phần trên có dạng hình nón bán kính đáy bằng R đã bị cắt bỏ bớt một phần hình nón có bán kính đáy bằng
1
2
R
ở phía trên (ngườ...
Đọc tiếp
Để định vị một trụ điện, người ta cần đúc một khối bê tông có chiều cao h = 1 , 5 m gồm:
- Phần dưới có dạng hình trụ bán kính đáy R = 1 m và có chiều cao bằng 1 3 h ;
- Phần trên có dạng hình nón bán kính đáy bằng R đã bị cắt bỏ bớt một phần hình nón có bán kính đáy bằng 1 2 R ở phía trên (người ta thường gọi hình đó là hình nón cụt);
- Phần ở giữa rỗng có dạng hình trụ bán kính đáy bằng 1 4 R (tham khảo hình vẽ bên dưới).
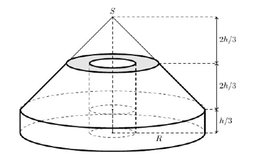
Thể tích của khối bê tông (làm tròn đến chữ số thập phân thứ ba) bằng
A. 2 , 815 m 3
B. 2 , 814 m 3
C. 3 , 403 m 3
D. 3 , 109 m 3
Một nhà máy cần sản suất các hộp hình trụ kín cả hai đầu có thể tích V cho trước. Mối quan hệ giữa bán kính đáy R và chiều cao h của hình trụ để diện tích toàn phần của hình trụ nhỏ nhất là ? A. R 2h B. h 2R C. h 3R D. R h
Đọc tiếp
Một nhà máy cần sản suất các hộp hình trụ kín cả hai đầu có thể tích V cho trước. Mối quan hệ giữa bán kính đáy R và chiều cao h của hình trụ để diện tích toàn phần của hình trụ nhỏ nhất là ?
A. R = 2h
B. h = 2R
C. h = 3R
D. R = h
Cho khối nón có bán kính đáy r 3, chiều cao
h
2
Tính thể tích V của khối nón. A.
V
3
π
2
3
B.
V
3
π
2
C.
V
9
π
2
3
D.
V...
Đọc tiếp
Cho khối nón có bán kính đáy r = 3, chiều cao h = 2 Tính thể tích V của khối nón.
A. V = 3 π 2 3
B. V = 3 π 2
C. V = 9 π 2 3
D. V = 9 π 2
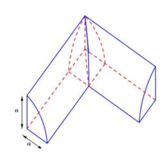
Cho hình lăng trụ tam giác đều
A
B
C
.
A
B
C
có độ dài cạnh đáy bằng a, chiều cao là h. Tính thể tích V của khối trụ ngoại tiếp hình lăng trụ. A.
V
π
a
2
h
9
B.
V
π
a
2...
Đọc tiếp
Cho hình lăng trụ tam giác đều A B C . A ' B ' C ' có độ dài cạnh đáy bằng a, chiều cao là h. Tính thể tích V của khối trụ ngoại tiếp hình lăng trụ.
A. V = π a 2 h 9
B. V = π a 2 h 3
C. V = 3 π a 2 h
D. V = π a 2 h
Gọi (H) là hình phẳng giới hạn bởi parabol (P):
y
8
x
-
x
2
và trục hoành. Các đường thẳng ya,yb,yc với 0abc16 chia (H) thành bốn phần có diện tích bằng nhau. Giá trị của biểu thức
(
16
-
a
)
3
+
(
16
-
b
)
3
+
(
16
-
c...
Đọc tiếp
Gọi (H) là hình phẳng giới hạn bởi parabol (P): y = 8 x - x 2 và trục hoành. Các đường thẳng y=a,y=b,y=c với 0<a<b<c<16 chia (H) thành bốn phần có diện tích bằng nhau. Giá trị của biểu thức ( 16 - a ) 3 + ( 16 - b ) 3 + ( 16 - c ) 3 bằng
A. 2048.
B. 3584.
C. 2816.
D. 3480.