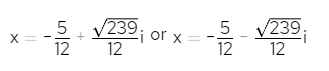Ta có:
\(\Delta'=\left(m-1\right)^2-\left(-2m-1\right)\)
\(=m^2-2m+1+2m+1\)
\(=m^2+2\)
Vì \(m^2+2>0,\forall m\)
\(\Rightarrow\) Pt luôn có hai nghiệm phân biệt \(x_1,x_2\)
Theo hệ thức Vi-ét, ta có: \(\left\{{}\begin{matrix}x_1+x_2=2\left(m-1\right)\left(1\right)\\x_1x_2=-2m-1\left(2\right)\end{matrix}\right.\)
Giả thiết: \(2x_1+3x_2+3x_1x_2=-11\)
\(\Leftrightarrow2\left(x_1+x_2\right)+x_2+3x_1x_2=-11\)
\(\Leftrightarrow2.2\left(m-1\right)+x_2+3\left(-2m-1\right)=-11\)
\(\Leftrightarrow4m-4+x_2-6m-3=-11\)
\(\Leftrightarrow x_2-2m-7=-11\)
\(\Leftrightarrow x_2=2m-4\)
Thay \(x_2=2m-4\) vào (1) ta được:
\(x_1+2m-4=2m-2\)
\(\Leftrightarrow x_1=2\)
Với \(x_1=2:x_2=2m-4\) vào (2) ta được:
\(2\left(2m-4\right)=-2m-1\)
\(\Leftrightarrow4m-8=-2m-1\)
\(\Leftrightarrow6m=7\)
\(\Leftrightarrow m=\dfrac{7}{6}\left(tm\right)\)
Vậy \(m=\dfrac{7}{6}\) thì pt có hai nghiệm thoả mãn: \(2x_1+3x_2+3x_1x_2=-11\)