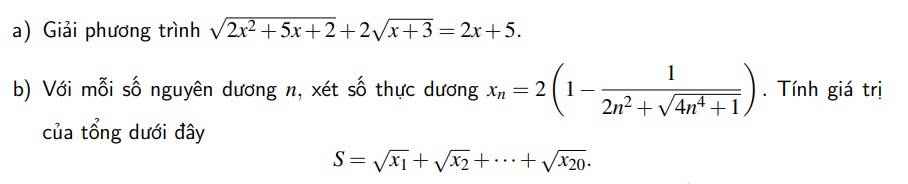\(a,\sqrt{2x^2+5x+2}+2\sqrt{x+3}=2x+5\)
dùng nhân lượng liên hợp cho bài này.
\(\cdot TXĐ:\left\{{}\begin{matrix}2x^2+5x+2\ge0\\x+3\ge0\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}-3\le x\le-2\\x\ge-\dfrac{1}{2}\end{matrix}\right.\)
\(\sqrt{2x^2+5x+2}+2\sqrt{x+3}=2x+5\)
\(\Leftrightarrow\sqrt{2x^2+5x+2}-3+2\left(\sqrt{x+3}-2\right)-2x+2=0\)
\(\Leftrightarrow\dfrac{2x^2+5x+2-9}{\sqrt{2x^2+5x+2}+3}+2.\dfrac{x+3-4}{\sqrt{x+3}+2}-2\left(x-1\right)=0\)
\(\Leftrightarrow\dfrac{\left(x-1\right)\left(2x+7\right)}{\sqrt{2x^2+5x+2}+3}+\dfrac{2\left(x-1\right)}{\sqrt{x+3}+2}-2\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(\dfrac{2x+7}{\sqrt{2x^2+5x+2}+3}+\dfrac{2}{\sqrt{x+3}+2}-2\right)=0\)
\(\left[{}\begin{matrix}x=1\left(nhận\right)\\\dfrac{2x+7}{\sqrt{2x^2+5x+2}+3}+\dfrac{2}{\sqrt{x+3}+2}-2>0\end{matrix}\right.\)
Vậy \(S=\left\{-1\right\}\)