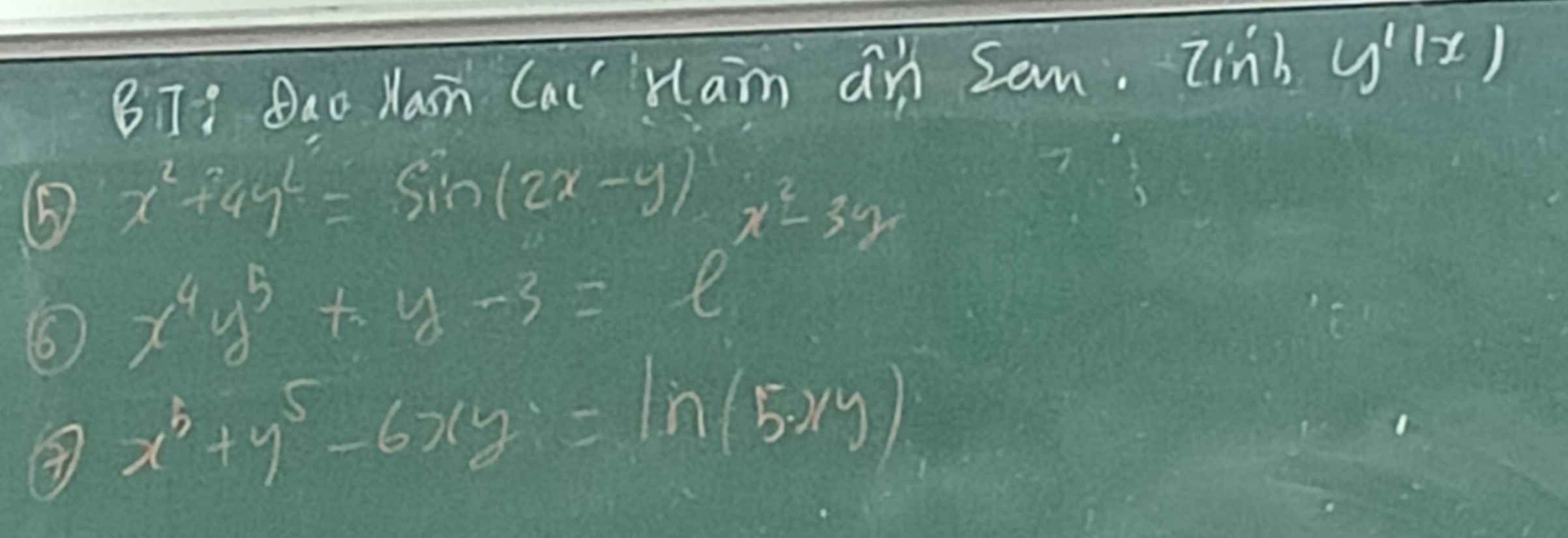5) \(...\Leftrightarrow2x+8y.y'\left(x\right)=\left[2-y'\left(x\right)\right]cos\left(2x-y\right)\)
\(\Leftrightarrow2x+8y.y'\left(x\right)=2cos\left(2x-y\right)-y'\left(x\right).cos\left(2x-y\right)\)
\(\Leftrightarrow y'\left(x\right)\left[8y+cos\left(2x-y\right)\right]=2\left[cos\left(2x-y\right)-1\right]\)
\(\Leftrightarrow y'\left(x\right)=\dfrac{2\left[cos\left(2x-y\right)-1\right]}{8y+cos\left(2x-y\right)}\)
6) \(...\Leftrightarrow4x^3y^5+5x^4y^4.y'\left(x\right)+y'\left(x\right)=\left[2x-3y'\left(x\right)\right]e^{x^2-3y}\)
\(\Leftrightarrow4x^3y^5+5x^4y^4.y'\left(x\right)+y'\left(x\right)=2x.e^{x^2-3y}-3y'\left(x\right).e^{x^2-3y}\)
\(\Leftrightarrow y'\left(x\right)\left[5x^4y^4+3e^{x^2-3y}+1\right]=2x.e^{x^2-3y}-4x^3y^5\)
\(\Leftrightarrow y'\left(x\right)=\dfrac{2x.\left(e^{x^2-3y}-2x^2y^5\right)}{5x^4y^4+3e^{x^2-3y}+1}\)
7) \(...\Leftrightarrow3x^2+5y^4.y'\left(x\right)-6y-6x.y'\left(x\right)=\dfrac{5y+5x.y'\left(x\right)}{5xy}=\dfrac{y+x.y'\left(x\right)}{xy}\)
\(\Leftrightarrow3x^3y+5xy^5.y'\left(x\right)-6xy^2-6x^2y.y'\left(x\right)=y+x.y'\left(x\right)\)
\(\Leftrightarrow y'\left(x\right)\left(5xy^5-6x^2y-x\right)=y+6xy^2-3x^3y\)
\(\Leftrightarrow y'\left(x\right)=\dfrac{y+6xy^2-3x^3y}{5xy^5-6x^2y-x}\)
\(\Leftrightarrow y'\left(x\right)=\dfrac{y\left(1+6xy-3x^3\right)}{x\left(5y^5-6xy-1\right)}\)