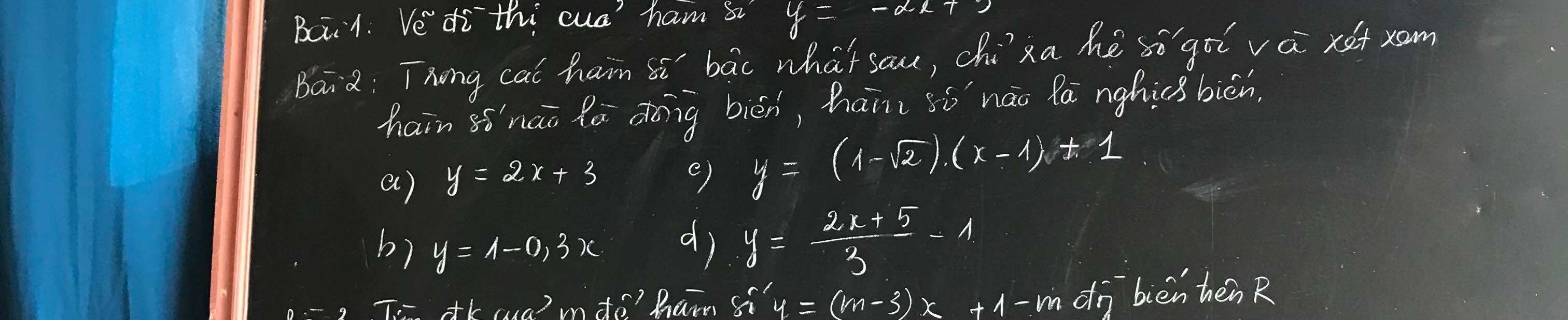a) \(ĐKXĐ:x\ge0;x\ne\pm9\).
\(A=\left(\dfrac{1}{\sqrt{x}-3}-\dfrac{1}{\sqrt{x}+3}\right):\dfrac{3}{\sqrt{x}-3}\)
\(=\dfrac{\sqrt{x}+3-\sqrt{x}+3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}.\dfrac{\sqrt{x}-3}{3}\)
\(=\dfrac{6}{3\left(\sqrt{x}+3\right)}=\dfrac{2}{\sqrt{x}+3}\)
b) \(A>\dfrac{1}{3}\)
\(\Rightarrow\dfrac{2}{\left(\sqrt{x}+3\right)}>\dfrac{1}{3}\)
\(\Leftrightarrow\dfrac{1}{\sqrt{x}+3}>\dfrac{1}{6}\)
Do \(\sqrt{x}+3>0\forall x>0\) nên bất phương trình tương đương:
\(0< \sqrt{x}+3< 6\)
\(\Leftrightarrow0\le\sqrt{x}< 3\)
\(\Leftrightarrow0\le\left|x\right|< 9\)
\(\Rightarrow0\le x< 9\) (do x không âm).
c) \(\sqrt{x}\ge0\Rightarrow\sqrt{x}+3\ge3\Rightarrow\dfrac{1}{\sqrt{x}+3}\le\dfrac{1}{3}\)
\(A=\dfrac{2}{\left(\sqrt{x}+3\right)}\le\dfrac{2}{\sqrt{0}+3}=\dfrac{2}{3}\)
Đẳng thức xảy ra khi \(\sqrt{x}=0\Leftrightarrow x=0\)
Vậy \(MaxA=\dfrac{2}{3}\) khi \(x=0\)



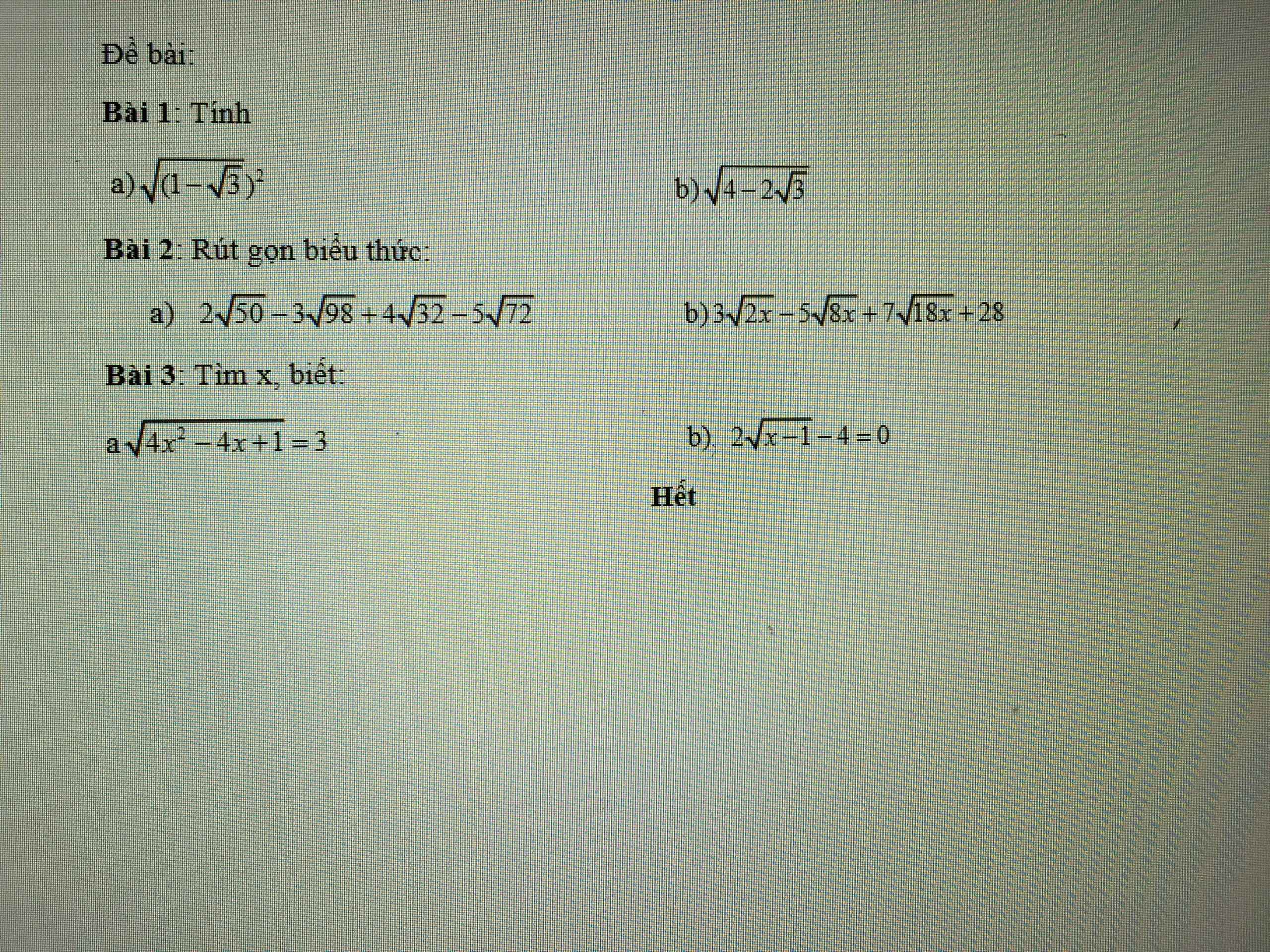 Giúp mình vs ạ. Cảm ơn trước ạ!
Giúp mình vs ạ. Cảm ơn trước ạ!