Lời giải:
Đa số các bài ntn thì hướng giải chung là xét trường hợp để phá dấu trị tuyệt đối.
a. $|2x-1|+|2x-5|=4$
Nếu $x\geq \frac{5}{2}$ thì $2x-1>0; 2x-5\geq 0$. Khi đó:
$2x-1+(2x-5)=4$
$4x-6=4$
$4x=10$
$x=\frac{10}{4}=2,5$ (thỏa mãn)
Nếu $\frac{1}{2}\leq x< \frac{5}{2}$ thì $2x-1\geq 0; 2x-5<0$. Khi đó:
$2x-1+(5-2x)=4$
hay $4=4$ (luôn đúng)
Nếu $x< \frac{1}{2}$ thì $2x-1<0; 2x-5<0$. Khi đó:
$1-2x+(5-2x)=4$
$6-4x=4$
$x=\frac{1}{2}$ (không tm)
Từ các TH đã xét suy ra mọi giá trị $x$ thỏa mãn $\frac{1}{2}\leq x\leq \frac{5}{2}$ thì thỏa mãn đề bài.
b. $|x-1|+|x-2|=3x+5$
Nếu $x\geq 2$ thì $x-1>0; x-2\geq 0$. Khi đó:
$x-1+x-2=3x+5$
$2x-3=3x+5$
$\Rightarrow x=-8$ (không tm)
Nếu $1\leq x< 2$ thì $x-1\geq 0; x-2<0$. Khi đó:
$x-1+2-x=3x+5$
$\Rightarrow 1=3x+5\Rightarrow x=\frac{-4}{3}$ (không tm)
Nếu $x<1$ thì $x-1<0; x-2<0$. Khi đó:
$1-x+2-x=3x+5$
$\Rightarrow 3-2x=3x+5$
$\Rightarrow x=-0,4$ (tm)
c.
$|2x-1|-6=0$
$|2x-1|=6$
$\Rightarrow 2x-1=6$ hoặc $2x-1=-6$
$\Rightarrow 2x=7$ hoặc $2x=-5$
$\Rightarrow x=\frac{7}{2}$ hoặc $x=\frac{-5}{2}$
d.
$|2x+1|=|-x|$
$\Rightarrow 2x+1=x$ hoặc $2x+1=-x$
$\Rightarrow x=-1$ hoặc $x=\frac{-1}{3}$
e. $|1-x|+|x+3|=x+5$
Nếu $x>1$ thì $1-x<0; x+3>0$ nên:
$x-1+x+3=x+5$
$\Rightarrow 2x+2=x+5$
$\Rightarrow x=3$ (tm)
Nếu $-3\leq x\leq 1$ thì $1-x\geq 0; x+3\geq 0$. Khi đó:
$1-x+x+3=x+5$
$\Rightarrow 4=x+5$
$\Rightarrow x=-1$ (tm)
Nếu $x< -3$ thì $1-x>0; x+3<0$. Khi đó:
$1-x+(-x-3)=x+5$
$\Rightarrow -2-2x=x+5$
$\Rightarrow -7=3x$
$\Rightarrow x=\frac{-7}{3}$ (không tm)
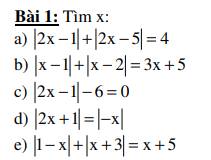










 giúp mình với ạ,mình xin cảm ơn trước
giúp mình với ạ,mình xin cảm ơn trước