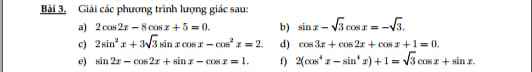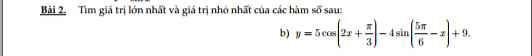a, \(2cos2x-8cosx+5=0\)
\(\Leftrightarrow4cos^2x-8cosx+3=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=\dfrac{4+\sqrt{10}}{2}\left(l\right)\\cosx=\dfrac{4-\sqrt{10}}{2}\end{matrix}\right.\)
\(\Leftrightarrow x=\pm arccos\left(\dfrac{4-\sqrt{10}}{2}\right)+k2\pi\)
b, \(sinx-\sqrt{3}cosx=-\sqrt{3}\)
\(\Leftrightarrow\dfrac{1}{2}sinx-\dfrac{\sqrt{3}}{2}cosx=-\dfrac{\sqrt{3}}{2}\)
\(\Leftrightarrow sin\left(x-\dfrac{\pi}{3}\right)=-\dfrac{\sqrt{3}}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{\pi}{3}=\dfrac{\pi}{3}+k2\pi\\x-\dfrac{\pi}{3}=\pi-\dfrac{\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{2\pi}{3}+k2\pi\\x=\pi+k2\pi\end{matrix}\right.\)
c, \(2sin^2x+3\sqrt{3}sinx.cosx-cos^2x=2\)
\(\Leftrightarrow4sin^2x-2+6\sqrt{3}sinx.cosx-2cos^2x+1=3\)
\(\Leftrightarrow3\sqrt{3}sin2x-3cos2x=3\)
\(\Leftrightarrow\dfrac{\sqrt{3}}{2}sin2x-\dfrac{1}{2}cos2x=\dfrac{1}{2}\)
\(\Leftrightarrow sin\left(2x-\dfrac{\pi}{6}\right)=\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-\dfrac{\pi}{6}=\dfrac{\pi}{6}+k2\pi\\2x-\dfrac{\pi}{6}=\pi-\dfrac{\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k\pi\\x=\dfrac{\pi}{2}+k\pi\end{matrix}\right.\)
d, \(cos3x+cos2x+cosx+1=0\)
\(\Leftrightarrow2cos2x.cosx+2cos^2x=0\)
\(\Leftrightarrow cosx\left(cos2x+cosx\right)=0\)
\(\Leftrightarrow2cosx.cos\dfrac{3x}{2}.cos\dfrac{x}{2}=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=0\\cos\dfrac{3x}{2}=0\\cos\dfrac{x}{2}=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k\pi\\\dfrac{3x}{2}=\dfrac{\pi}{2}+k\pi\\\dfrac{x}{2}=\dfrac{\pi}{2}+k\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k\pi\\x=\dfrac{\pi}{3}+\dfrac{k2\pi}{3}\\x=\pi+k2\pi\end{matrix}\right.\)
e, \(sin2x-cos2x+sinx-cosx=1\)
\(\Leftrightarrow2sinx.cosx-2cos^2x+sinx-cosx=0\)
\(\Leftrightarrow2cosx\left(sinx-cosx\right)+sinx-cosx=0\)
\(\Leftrightarrow\left(sinx-cosx\right)\left(2cosx-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=cosx\\cosx=\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+k\pi\\x=\pm\dfrac{\pi}{6}+k2\pi\end{matrix}\right.\)
f, \(2\left(cos^4x-sin^4x\right)+1=\sqrt{3}cosx+sinx\)
\(\Leftrightarrow2\left(cos^2x-sin^2x\right)\left(cos^2x+sin^2x\right)+1=\sqrt{3}cosx+sinx\)
\(\Leftrightarrow2cos2x+1=\sqrt{3}cosx+sinx\)
\(\Leftrightarrow cos2x+\dfrac{1}{2}=\dfrac{\sqrt{3}}{2}cosx+\dfrac{1}{2}sinx\)
\(\Leftrightarrow cos2x+cos\dfrac{\pi}{3}=\dfrac{\sqrt{3}}{2}cosx+\dfrac{1}{2}sinx\)
\(\Leftrightarrow2cos\left(x+\dfrac{\pi}{6}\right).cos\left(x-\dfrac{\pi}{6}\right)=cos\left(x-\dfrac{\pi}{6}\right)\)
\(\Leftrightarrow\left[2cos\left(x+\dfrac{\pi}{6}\right)-1\right].cos\left(x-\dfrac{\pi}{6}\right)=\text{}0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos\left(x+\dfrac{\pi}{6}\right)=\dfrac{1}{2}\\cos\left(x-\dfrac{\pi}{6}\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{2\pi}{3}+k\pi\\x=\dfrac{\pi}{6}+k2\pi\\x=\dfrac{\pi}{2}+k2\pi\end{matrix}\right.\)