`!`
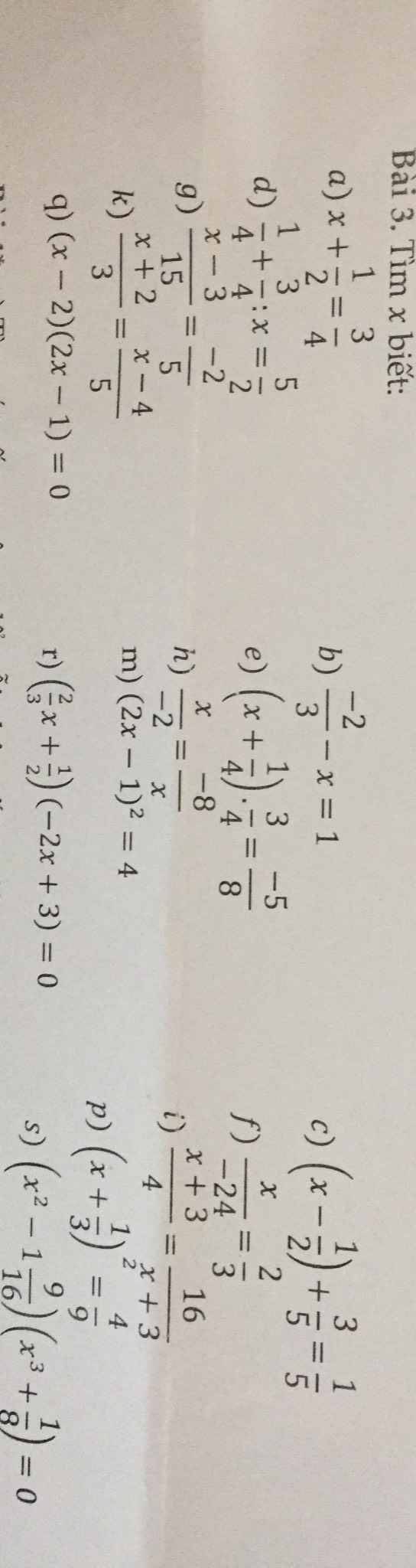
`a, x+1/2=3/4`
`=>x=3/4-1/2`
`=>x=3/4-2/4`
`=>x=1/4`
`b, -2/3-x=1`
`=> x=-2/3-1`
`=>x=-2/3 -3/3`
`=>x=-5/3`
`c, (x-1/2)+3/5=1/5`
`=>x-1/2=1/5-3/5`
`=>x-1/2=-2/5`
`=>x=-2/5+1/2`
`=>x= 1/10`
`d, 1/4+3/4 :x=5/2`
`=> 3/4 :x=5/2-1/4`
`=> 3/4 :x=9/4`
`=>x= 3/4 : 9/4`
`=>x= 3/4 . 4/9`
`=>x= 1/3`
`e, (x+1/4).3/4=-5/8`
`=> x+1/4=-5/8 : 3/4`
`=> x+1/4=-5/8 . 4/3`
`=> x+1/4=-5/6`
`=>x=-5/6 -1/4`
`=>x= -13/12`
`f, x/(-24) =2/3`
`=> 3x=2.(-24)`
`=> 3x=-48`
`=>x=-48:3`
`=>x= -16`
Bn tách ra nữa nha , nhiều quá á
`!`
`g, (x-3)/15=-2/5`
`=> (x-3).5= 15.(-2)`
`=> (x-3).5= -30`
`=>x-3=-30:5`
`=>x-3=-6`
`=>x=-6+3`
`=>x=-3`
`h, x/(-2)=-8/x`
`=> x.x=-2.(-8)`
`=>x^2 =16`
\(\Rightarrow x=\left[{}\begin{matrix}4\\-4\end{matrix}\right.\)
`i, (x+3)/4 =16/(x+3)`
`=> (x+3)^2 =4.16`
`=> (x+3)^2 = 64`
`=> (x+3)^2 = +-8^2`
\(\Rightarrow\left[{}\begin{matrix}x+3=8\\x+3=-8\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=5\\x=-11\end{matrix}\right.\)
`k, (x+2)/3=(x-3)/5`
`=> (x+2).5 = 3(x-3)`
`=> 5x+10 = 3x-9`
`=> 5x-3x=9-10`
`=> 2x= -1`
`=>x=-1/2`
`m, (2x-1)^2=4`
`=> (2x-1)^2= +-2^2`
\(\Rightarrow\left[{}\begin{matrix}2x-1=2\\2x-1=-2\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}2x=3\\2x=-1\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=-\dfrac{1}{2}\end{matrix}\right.\)
`p, (x+1/3)^2=4/9`
`=> (x+1/3)^2=(+- 2/3)^2`
\(\Rightarrow\left[{}\begin{matrix}x+\dfrac{1}{3}=\dfrac{2}{3}\\x+\dfrac{1}{3}=-\dfrac{2}{3}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{1}{3}\\x=-1\end{matrix}\right.\)
`q , (x-2)(2x-1)=0`
`@ TH1`
`x-2=0`
`=>x=0+2`
`=>x=2`
`@ TH2`
`2x-1=0`
`=>2x=0+1`
`=>2x=1`
`=>x=1/2`
`r, (2/3x +1/2)(-2x+3)=0`
`@ TH1`
`2/3x+1/2=0`
`=>2/3x=0-1/2`
`=>2/3x=-1/2`
`=>x=-1/2 : 2/3`
`=>x= -1/12`
`@ TH2`
`-2x+3=0`
`=> -2x=0-3`
`=>-2x=-3`
`=>x=3/2`
`s, (x^2 - 1 9/16 )(x^3+1/8)=0`
`@ TH1`
`x^2 -1 9/16=0`
`=>x^2 - 25/16=0`
`=>x^2=25/16`
`=>x^2=(+- 5/4)^2`
`=> x=(+-5/4)`
`@ TH2`
`x^3+1/8=0`
`=>x^3=1/8`
`=>x^3= (1/2)^3`
`=>x=1/2`