\(\dfrac{xy}{x^2+y^2-z^2}+\dfrac{xz}{x^2+z^2-y^2}+\dfrac{yz}{y^2+z^2-x^2}\)
\(=\dfrac{xy}{\left(x+y\right)^2-z^2-2xy}+\dfrac{xz}{\left(x+z\right)^2-y^2-2xz}+\dfrac{yz}{\left(y+z\right)^2-x^2-2yz}\)
\(=\dfrac{xy}{\left(x+y-z\right)\left(x+y+z\right)-2xy}+\dfrac{xz}{\left(x+z-y\right)\left(x+z+y\right)-2xz}+\dfrac{yz}{\left(y+z-x\right)\left(y+x+z\right)-2yz}\)
\(=\dfrac{xy}{-2xy}+\dfrac{xz}{-2xz}+\dfrac{yz}{-2yz}=-\dfrac{1}{2}-\dfrac{1}{2}-\dfrac{1}{2}=-\dfrac{3}{2}\)
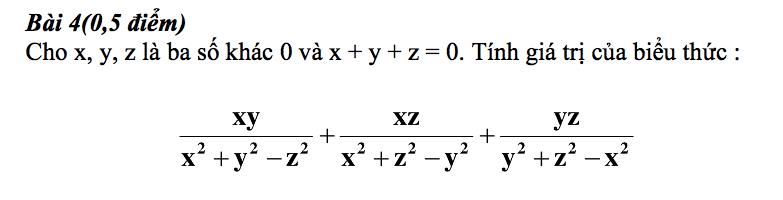 Giúp mình với ạ
Giúp mình với ạ


