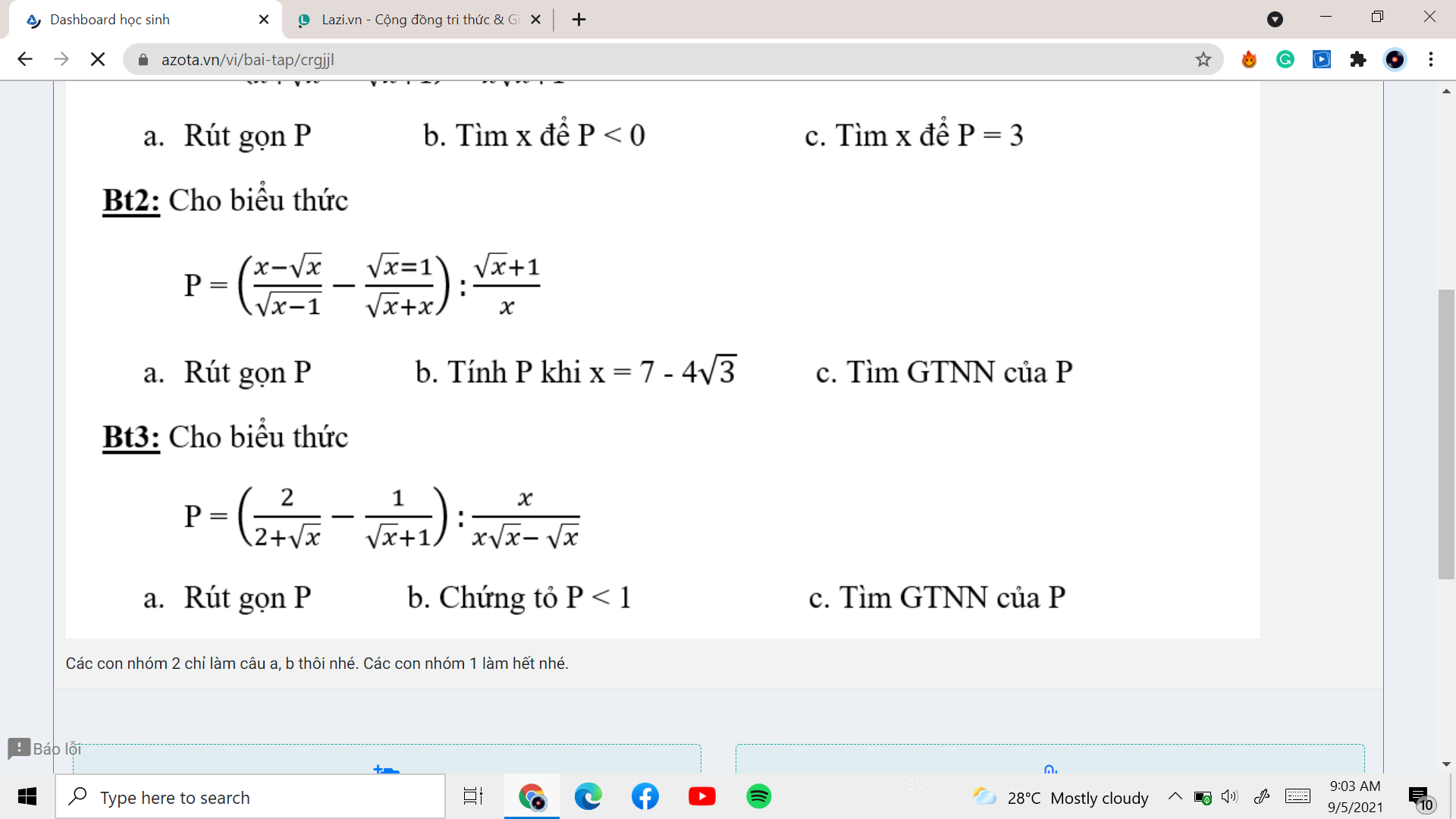
a, ĐKXĐ : \(\left\{{}\begin{matrix}x>0\\x\ne4\end{matrix}\right.\)
b, Ta có : \(P=\left(\dfrac{1}{\sqrt{x}-2}-\dfrac{1}{\sqrt{x}+2}\right)\left(1-\dfrac{2}{\sqrt{x}}\right)\)
\(=\left(\dfrac{\sqrt{x}+2-\sqrt{x}+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\right)\left(\dfrac{\sqrt{x}-2}{\sqrt{x}}\right)\)
\(=\dfrac{4\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)\sqrt{x}}=\dfrac{4}{\sqrt{x}\left(\sqrt{x}+2\right)}\)
c, Ta có : \(x=4-2\sqrt{3}=3-2\sqrt{3}+1=\left(\sqrt{3}-1\right)^2\)
- Thay x vào A ta được : \(A=\dfrac{4}{\left(\sqrt{3}-1\right)\left(\sqrt{3}-1+2\right)}\)
\(=\dfrac{4}{\left(\sqrt{3}-1\right)\left(\sqrt{3}+1\right)}=\dfrac{4}{3-1}=\dfrac{4}{2}=2\)
`2a)ĐKXĐ:` \(\begin{cases}x \ge 0\\\sqrt{x}-2 \ne 0\\\end{cases}\)
`<=>` \(\begin{cases}x \ge 0\\x \ne 4\\\end{cases}\)
`b)P=(1/(sqrtx-2)-1/(sqrtx+2))(1-2/sqrtx)`
`=((sqrtx+2-sqrtx+2)/(x-4))((sqrtx-2)/sqrtx)`
`=4/(x-4)*(sqrtx-2)/sqrtx`
`=4/(sqrtx(sqrtx+2))`
`c)x=4-2sqrt3`
`=3-2sqrt3+1=(sqrt3-1)^2`
`=>P=4/((sqrt3-1)(sqrt3-1+2))`
`=4/((sqrt3-1)(sqrt3+1))`
`=4/(3-1)=4/2=2`
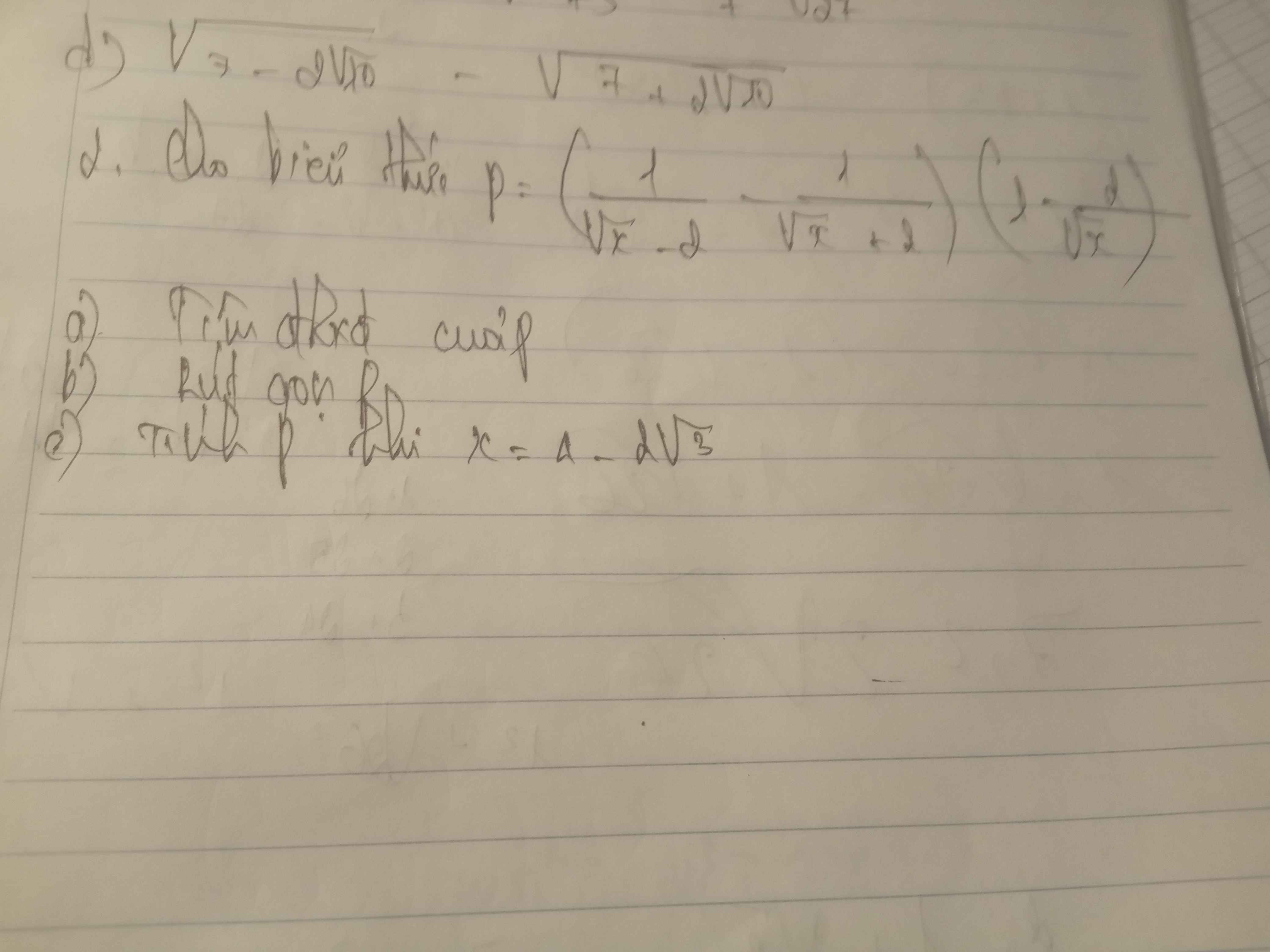







 Giải giúp mình bài 1 bài 2 đi mn
Giải giúp mình bài 1 bài 2 đi mn