Bài 2
a) Để P có nghĩa
\(\Leftrightarrow\left\{{}\begin{matrix}\sqrt{x}\ge0\\\sqrt{x}-1\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\\sqrt{x}\ne1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\x\ne1\end{matrix}\right.\)
vậy để P có nghĩ thì \(x\ge0;x\ne1\)
b) \(P=\left(\dfrac{\sqrt{x}}{\sqrt{x}+1}-\dfrac{\sqrt{x}}{\sqrt{x}-1}\right):\dfrac{-2\sqrt{x}}{\sqrt{x}-1}\)
\(=\left(\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{x-1}-\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{x-1}\right).\dfrac{\sqrt{x}-1}{-2\sqrt{x}}\)
\(=\dfrac{x-\sqrt{x}-x-\sqrt{x}}{x-1}.\dfrac{\sqrt{x}-1}{-2\sqrt{x}}\)
\(=\dfrac{-2\sqrt{x}}{x-1}.\dfrac{\sqrt{x}-1}{-2\sqrt{x}}\)
\(\dfrac{1}{\sqrt{x}+1}\)
Đúng 1
Bình luận (0)
Các câu hỏi tương tự
Mn giúp mình giải bài 3 và 4 với ạ mình cảm ơn mn mong mn giúp 🥺
Giúp Mình Làm Bài 2 Với Ạ🥺🙏
Giúp Mình Bài 4 Với Ạ🥺
 Ai giúp mình giải câu 3 với,mình cảm ơn nhìuuuu ạ 🥺
Ai giúp mình giải câu 3 với,mình cảm ơn nhìuuuu ạ 🥺
Giúp Mình 2 Câu Này Với Ạ🥺♥️✨
Giúp mình làm với ạ 🥺
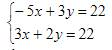 ai giúp em bài này với ạ 🥺 :)
ai giúp em bài này với ạ 🥺 :)
Giải giúp mình phần tự luận với ạ🥺
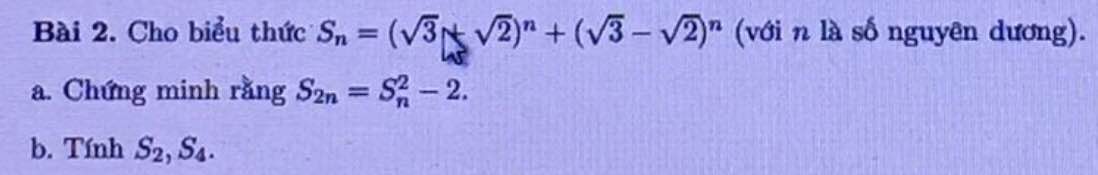 mọi người giải giúp em bài này với ạ 🥺
mọi người giải giúp em bài này với ạ 🥺
mn ơi giải giúp em bài này với ạ 🥺🙏


