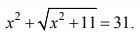Question

Giúp mik vs, thks

Answer 1

`x^2+\sqrt{x^2+11}=31`

`<=>x^2+11+\sqrt{x^2+11}-42=0`

Đặt `\sqrt{x^2+11}=t` `(t >= 0)` khi đó ptr có dạng:

     `t^2+t-42=0`

`<=>t^2+7t-6t-42=0`

`<=>t(t+7)-6(t+7)=0`

`<=>(t+7)(t-6)=0`

`<=>` $\left[\begin{matrix} t=-7\text{ (ko t/m)}\\ t=6\text{ (t/m)}\end{matrix}\right.$

   `@` Với `t=6=>\sqrt{x^2+11}=6`

                     `<=>x^2+11=36`

                      `<=>x^2=25`

                      `<=>x=+-5`

Vậy `S={+-5}`

Answer 2

`x^2 + sqrt(x^2+11) = 31`.

`=> (x^2+11) + sqrt(x^2+11) - 42 = 0`

Đặt `sqrt(x^2+11) = 1 ( x>=0)`.

Khi đó, phương trình trở thành:

`t^2 + t - 42 = 0`

`=> (t+7)(t-6) = 0`

`=> t = -7 (ktm)`

     `t = 6 ( tm)`

Khi `t = 6 => sqrt(x^2+11) = 6`

`=> x^2 + 11 = 36`

`=> x^2 = 25`

`=> x = +-5`.