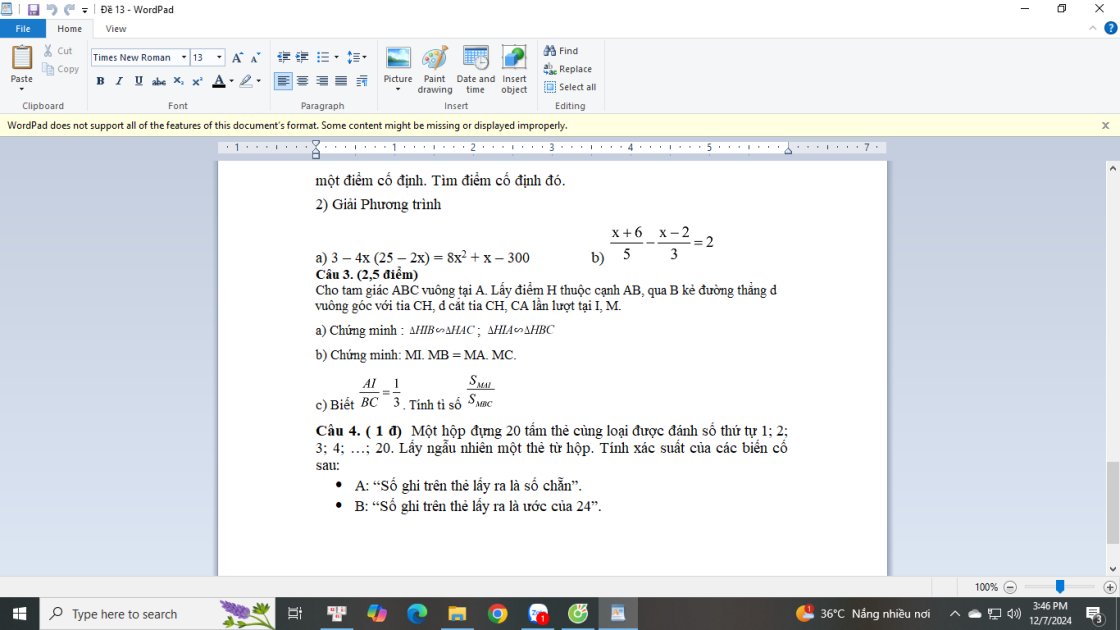
Câu2
a, \(3-4x\left(25-2x\right)=8x^2+x-300\)
\(\Leftrightarrow3-100x+8x^2=8x^2+x-300\Leftrightarrow101x=303\Leftrightarrow x=3\)
b, \(\dfrac{x+6}{5}-\dfrac{x-2}{3}=2\Rightarrow3\left(x+6\right)-5\left(x-2\right)=2.15\)
\(\Leftrightarrow3x+18-5x+10=30\Leftrightarrow-2x=2\Leftrightarrow x=-1\)
Bài 3 :
a, Xét tam giác HIB và tam giác HAC ta có
^IHB = ^AHC ( đối đỉnh )
^HIB = ^HAC = 900
Vậy tam giác HIB ~ tam giác HAC (g.g)
=> \(\dfrac{HB}{HC}=\dfrac{HI}{HA}\Rightarrow\dfrac{HI}{HB}=\dfrac{HA}{HC}\)
Xét tam giác HIA và tam giác HBC ta có
^IHA = ^BHC ( đối đỉnh )
\(\dfrac{HI}{HB}=\dfrac{HA}{HC}\)(cmt)
Vậy tam giác HIA ~ tam giác HBC (c.g.c)
b, tam giác HIA ~ tam giác HBC (cmt)
=> ^HIA = ^HBC
mà ^HIA phụ với ^AIH; ^HCB phụ với ^HBC
=> ^MIA = ^MCB
Xét tam giác MIA và tam giác MCB ta có
^MIA = ^MCB (cmt)
^IMA_chung
Vậy tam giác MIA ~ tam giác MCB (g.g)
\(\dfrac{MI}{MC}=\dfrac{MA}{MB}\Rightarrow MI.MB=MA.MC\)
c, Ta có \(\dfrac{S_{MAI}}{S_{MBC}}=\left(\dfrac{AI}{BC}\right)^2=\dfrac{1}{9}\)
Bài 4
a, A'' Số ghi trên thẻ lấy ra là chẵng''
A={2;4;6;8;10;12;14;16;18;20}
n(A) = 10
=> P(A) = n(A)/n(ko gian mẫu) = 10/20 =1/2
b, B''Số ghi trên thẻ lấy ra ước của 24''
B = {1;2;3;4;6;8;12}
n(B) = 7
=> P(B) = n(B)/n(ko gian mẫu) = 7/20