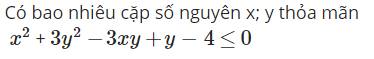a) PT \(\Leftrightarrow\left(x^2-y\right)\left(x^2+y+1\right)=-20\)
\(\Leftrightarrow\left(y-x^2\right)\left(y+x^2+1\right)=20\).
Do \(y-x^2< y+x^2+1\) và \(y-x^2\); \(y+x^2+1\) khác tính chẵn, lẻ nên ta có các trường hợp:
+) \(\left\{{}\begin{matrix}y-x^2=1\\y+x^2+1=20\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}y=10\\x^2=9\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}y=10\\x=\pm3\end{matrix}\right.\)
+) \(\left\{{}\begin{matrix}y-x^2=4\\y+x^2+1=5\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}y=4\\x^2=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}y=4\\x=0\end{matrix}\right.\)
+) \(\left\{{}\begin{matrix}y-x^2=-20\\y+x^2+1=-1\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}y=-11\\x^2=9\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}y=-11\\x=\pm3\end{matrix}\right.\)
+) \(\left\{{}\begin{matrix}y-x^2=-5\\y+x^2+1=-4\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}y=-5\\x^2=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}y=-5\\x=0\end{matrix}\right.\)
Vậy....







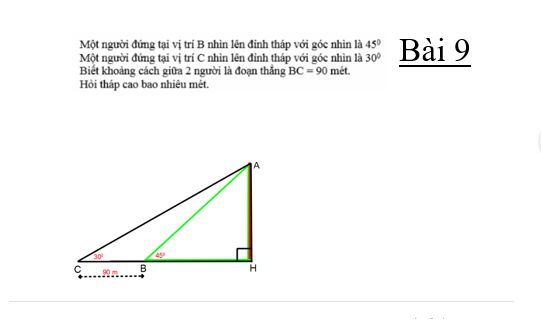 giúp em với ạ. Em cảm ơn ạ
giúp em với ạ. Em cảm ơn ạ