Câu 1:
\(\sqrt{a^2+b^2}\ge\dfrac{a+b}{\sqrt{2}}\\ \Leftrightarrow\sqrt{2a^2+2b^2}\ge a+b\\ \Leftrightarrow2a^2+2b^2\ge a^2+2ab+b^2\\ \Leftrightarrow a^2-2ab+b^2\ge0\\ \Leftrightarrow\left(a-b\right)^2\ge0\left(luôn.đúng\right)\)
Vậy \(\sqrt{a^2+b^2}\ge\dfrac{a+b}{\sqrt{2}}\), dấu \("="\Leftrightarrow a=b\)
Bạn kham khảo
`\sqrt{a^+b^2}>=(a+b)/(\sqrt{2})`
`<=>\sqrt{2a^2+2b^2}>=a+b`
`<=>2a^2+2b^2>=a^2+2ab+b^2`
`<=>a^2-acb+b^2>=0`
`<=>(a-b)^2>=0`(luôn đúng)
Dấu "=" xảy ra khi
`a=b`





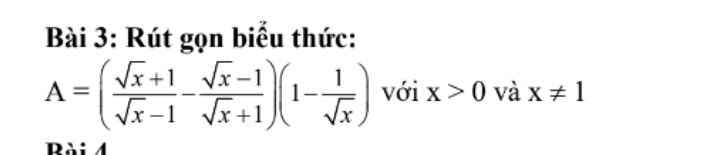




 Em cần giúp câu c và d ạ, mn giúp em với em đang cần gấp
Em cần giúp câu c và d ạ, mn giúp em với em đang cần gấp

