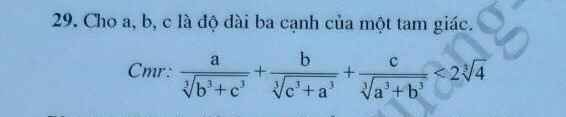Đặt \(\left\{{}\begin{matrix}\dfrac{x}{1-x}=a>0\\\dfrac{y}{1-y}=b>0\\\dfrac{z}{1-z}=c>0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=a-ax\\y=b-by\\z=c-cz\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{a}{a+1}\\y=\dfrac{b}{b+1}\\z=\dfrac{c}{c+1}\end{matrix}\right.\)
Bài toán trở thàn: cho \(\dfrac{a}{a+1}+\dfrac{b}{b+1}+\dfrac{c}{c+1}=2\), tìm min \(P=abc\)
Ta có:
\(\dfrac{a}{a+1}=1-\dfrac{b}{b+1}+1-\dfrac{c}{c+1}=\dfrac{1}{b+1}+\dfrac{1}{c+1}\ge\dfrac{2}{\sqrt{\left(b+1\right)\left(c+1\right)}}\)
Tương tự:
\(\dfrac{b}{b+1}\ge\dfrac{2}{\sqrt{\left(a+1\right)\left(c+1\right)}}\) ; \(\dfrac{c}{c+1}\ge\dfrac{2}{\sqrt{\left(a+1\right)\left(b+1\right)}}\)
Nhân vế và rút gọn;
\(abc\ge8\Rightarrow P_{min}=8\) khi \(a=b=c=2\) hay \(x=y=z=\dfrac{2}{3}\)
đặt \(\left\{{}\begin{matrix}1-x=a\\1-y=b\\1-z=c\end{matrix}\right.=>\left\{{}\begin{matrix}x=1-a\\y=1-b\\z=1-c\end{matrix}\right.\) với a+b+c=1
\(=>P=\dfrac{1-a}{a}+\dfrac{1-b}{b}+\dfrac{1-c}{c}=\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}-3\)
áp dụng BDT Cauchy schawarz
\(=>\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}-3\ge\dfrac{\left(1+1+1\right)^2}{a+b+c}-3=9-3=6\)
dấu"=" xảy ra<=>\(a=b=c=\dfrac{1}{3}< =>x=y=z=\dfrac{2}{3}\)