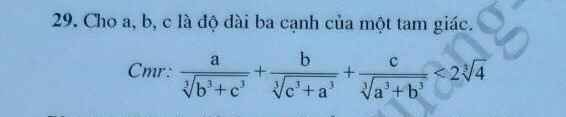Ta có:
\(\left(\dfrac{a^3}{b^3+c^3}+\dfrac{b^3}{c^3+a^3}+\dfrac{c^3}{a^3+b^3}\right)\left(1+1+1\right)\left(1+1+1\right)\ge\left(\sqrt[3]{\dfrac{a^3}{b^3+c^3}}+\sqrt[3]{\dfrac{b^3}{c^3+a^3}}+\sqrt[3]{\dfrac{c^3}{a^3+b^3}}\right)^3\)
\(\Leftrightarrow\sqrt[3]{\dfrac{a^3}{b^3+c^3}}+\sqrt[3]{\dfrac{b^3}{c^3+a^3}}+\sqrt[3]{\dfrac{c^3}{a^3+b^3}}\le\sqrt[3]{9\left(\dfrac{a^3}{b^3+c^3}+\dfrac{b^3}{c^3+a^3}+\dfrac{c^3}{a^3+b^3}\right)}\)
\(< \sqrt[3]{9\left(\dfrac{2a^3}{a^3+b^3+c^3}+\dfrac{2b^3}{a^3+b^3+c^3}+\dfrac{2c^3}{a^3+b^3+c^3}\right)}=\sqrt[3]{18}< \sqrt[3]{32}=2\sqrt[3]{4}\)