Lời giải:
a. Gọi 3 số tự nhiên liên tiếp là $a, a+1, a+2$. Tổng của 3 số là:
$a+(a+1)+(a+2)=3a+3=3(a+1)\vdots 3$
Ta có đpcm.
b.
Gọi 2 số chẵn liên tiếp là $2k+2$ và $2k+4$ với $k$ là số tự nhiên.
Tổng 2 số chẵn liên tiếp là:
$2k+2+2k+4=4k+6=4(k+1)+2$ chia 4 dư 2 (tức là không chia hết cho 4)
Do đó ta có đpcm.
c.
Trong 2 số tự nhiên liên tiếp luôn tồn tại 1 số chẵn và 1 số lẻ. Do đó tích của chúng sẽ luôn là số chẵn (chia hết cho 2), vì chẵn x lẻ = chẵn.
d. Gọi 3 số tự nhiên liên tiếp là $a, a+1, a+2$
Nếu $a$ chia hết cho 3 thì $a(a+1)(a+2)\vdots 3$
Nếu $a$ chia 3 dư 1 thì $a+2\vdots 3\Rightarrow a(a+1)(a+2)\vdots 3$
Nếu $a$ chia 3 dư 2 thì $a+1\vdots 3\Rightarrow a(a+1)(a+2)\vdots 3$
Vậy $a(a+1)(a+2)$ luôn chia hết cho 3 trong mọi trường hợp
Do đó ta có đpcm.



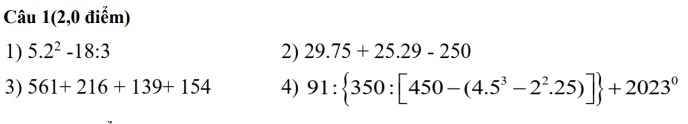
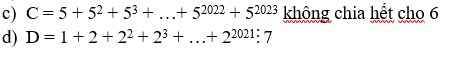
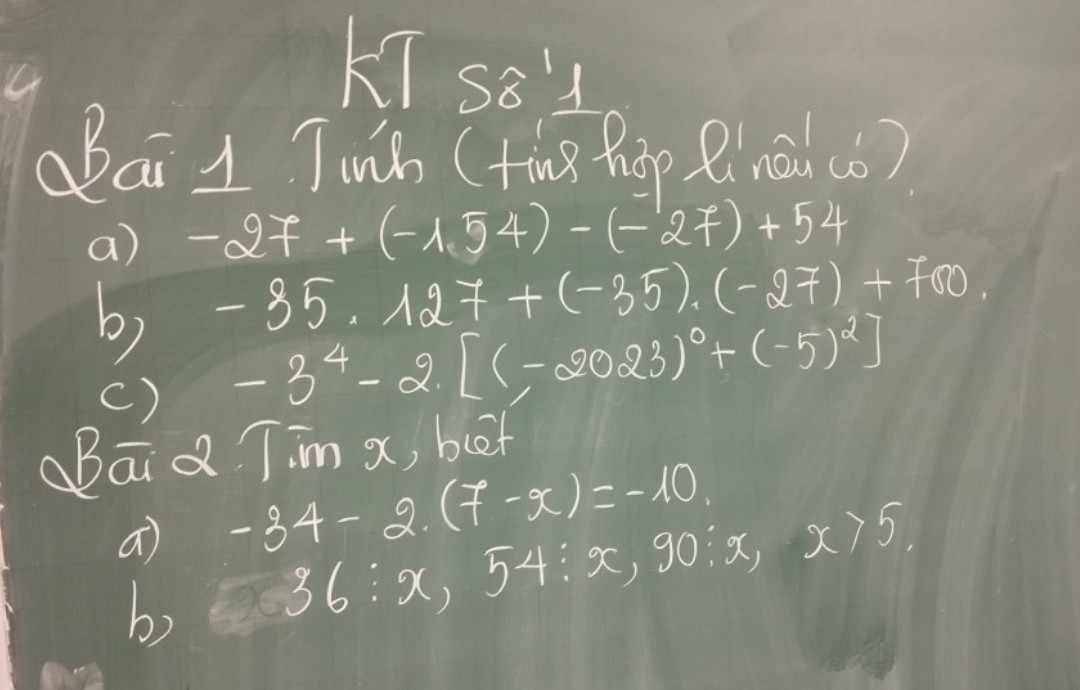
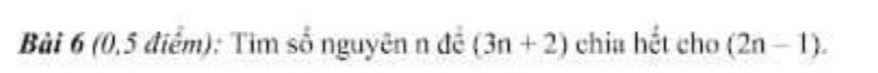 mn giúp em với ạ, em đang cần gấp lắm ạ
mn giúp em với ạ, em đang cần gấp lắm ạ

