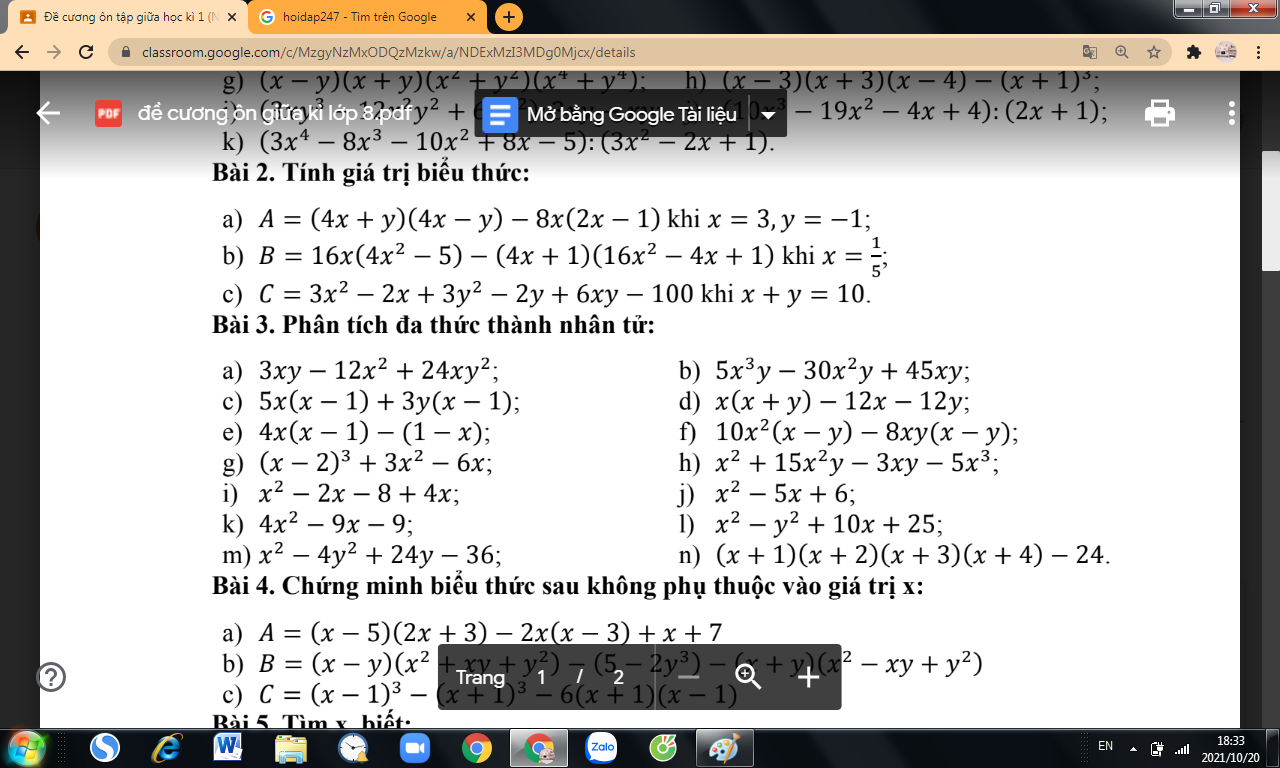
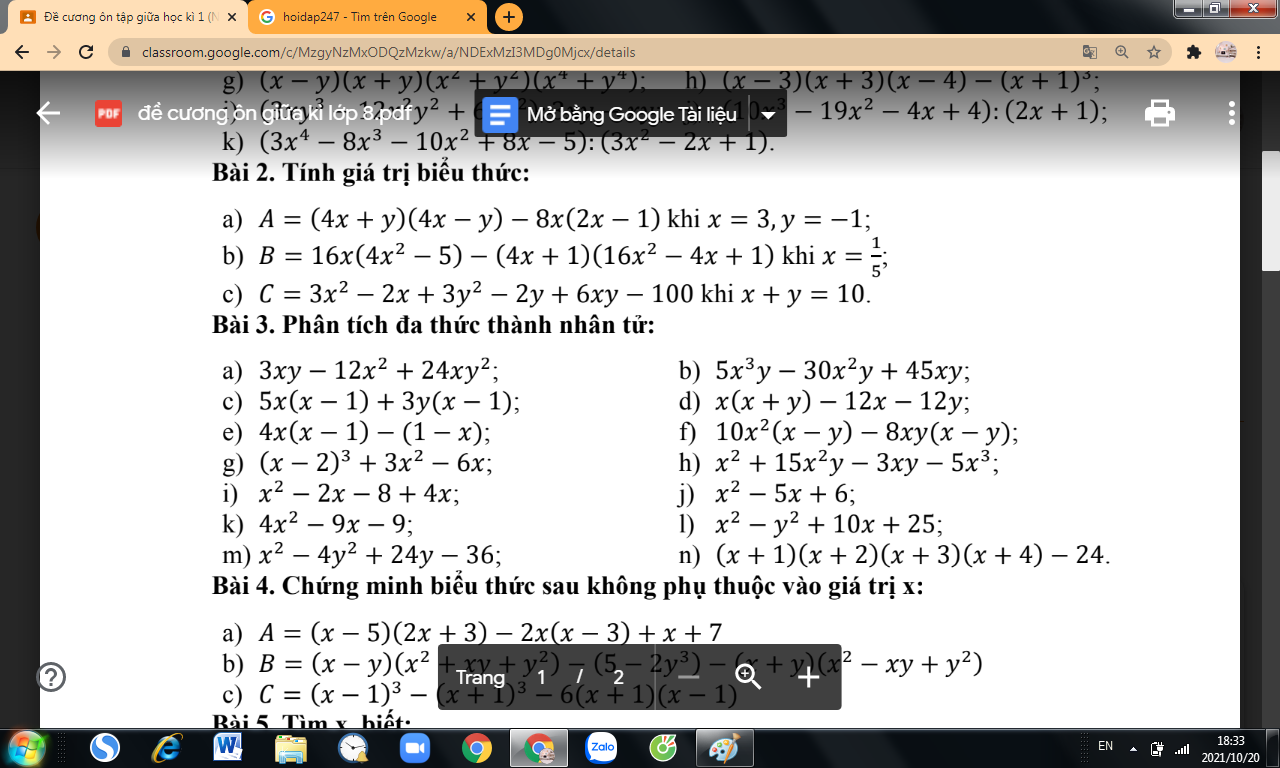
\(\left(\dfrac{8}{\left(x-4\right)\left(x+4\right)}+\dfrac{1}{x+4}\right):\dfrac{1}{x^2-4x+2x-8}\)
\(\left(\dfrac{8}{\left(x-4\right)\left(x+4\right)}+\dfrac{x-4}{\left(x-4\right)\left(x+4\right)}\right):\dfrac{1}{x\left(x-4\right)+2\left(x-4\right)}\)
\(\dfrac{8+x-4}{\left(x-4\right)\left(x+4\right)}:\dfrac{1}{\left(x-4\right)\left(x+2\right)}=\dfrac{x+4}{\left(x-4\right)\left(x+4\right)}:\dfrac{1}{\left(x-4\right)\left(x+2\right)}\)
\(\dfrac{\left(x+4\right)\left(x-4\right)\left(x+2\right)}{\left(x-4\right)\left(x+4\right)}=x+2\)
\(x^2-9x+20=0\\ x^2-4x-5x+20=0\\ x\left(x-4\right)-5\left(x-4\right)=0\\ \left(x-4\right)\left(x-5\right)=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-4=0\\x-5=0\end{matrix}\right.\)
=> x=4 hoặc x=5 tại bt \(x^2-9x+20=0\)



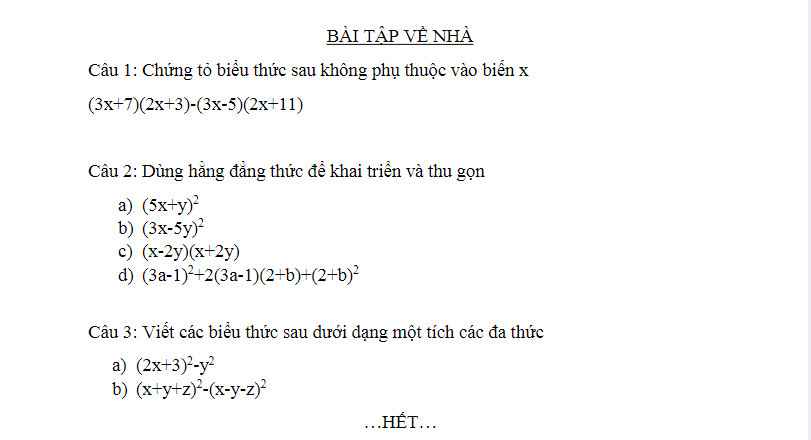




 em cần giải gấp bài 3 chi tiết mọi người giúp em với ạ. Làm bài dưới dạng phân số ạ em cần gấp
em cần giải gấp bài 3 chi tiết mọi người giúp em với ạ. Làm bài dưới dạng phân số ạ em cần gấp