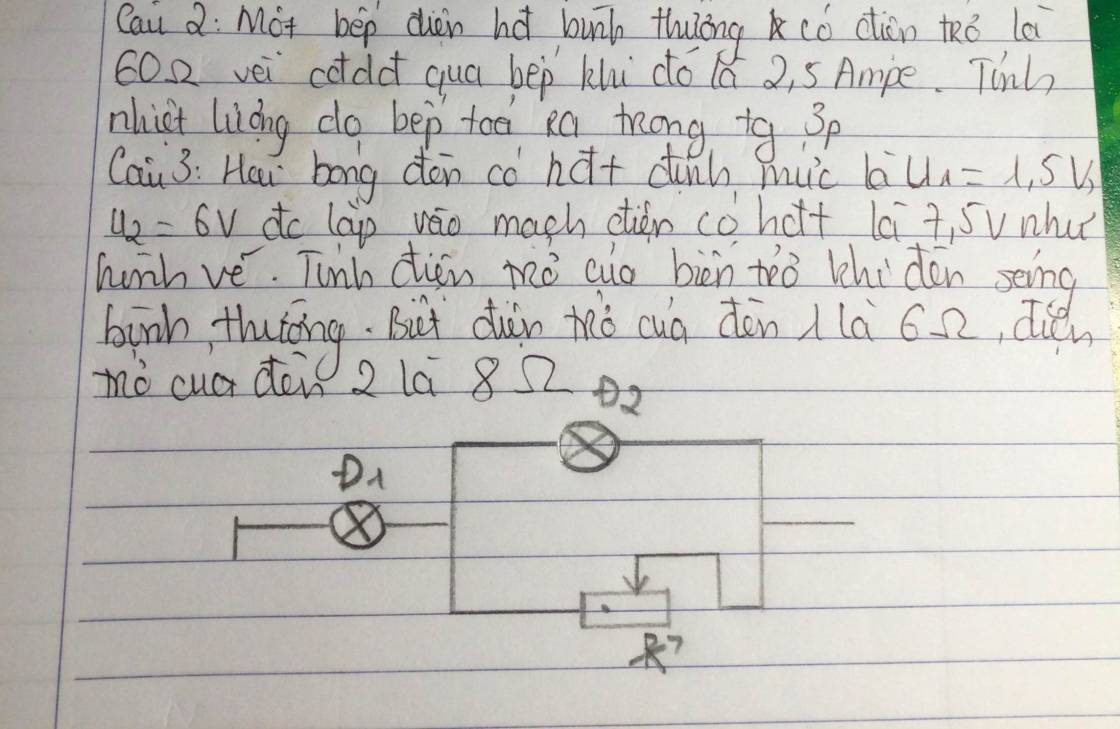
a)\(R_Đ=\dfrac{U^2_Đ}{P_Đ}=\dfrac{6^2}{9}=4\Omega\)
Đèn sáng bình thường: \(I_m=I_{Đđm}=\dfrac{P_Đ}{U_Đ}=\dfrac{9}{6}=1,5A\)
\(R_{tđ}=\dfrac{U}{I}=\dfrac{9}{1,5}=6\Omega\)
\(\Rightarrow R_{1x}=R_{tđ}-R_Đ=6-4=2\Omega\)
Mà \(\dfrac{1}{R_{1x}}=\dfrac{1}{R_1}+\dfrac{1}{R_x}=\dfrac{1}{16}+\dfrac{1}{R_x}=\dfrac{1}{2}\)
\(\Rightarrow R_x=\dfrac{16}{7}\Omega\)
b) đợi mình chút nhé
b)\(U_x=U_1=U-U_Đ=9-6=3V\)
Công suất tiêu thụ trên \(R_x\): \(P_x=I_x^2\cdot R_x=R_x\cdot\dfrac{U^2}{\left(R_1+R_x\right)^2}=R_x\cdot\dfrac{U^2}{R_1^2+2R_1\cdot R_x+R_x^2}=R_x\cdot\dfrac{U^2}{\dfrac{R_1^2}{R_x}+2R_1+R_x}\)\(P_xmax\Leftrightarrow\left(\dfrac{R_1^2}{R_x}+R_x\right)min\)
Theo BĐT Coossy:
\(\dfrac{R_1^2}{R_x}+R_x\ge2\sqrt{R_1}=2\sqrt{16}=8\)
\(\Rightarrow\dfrac{R_Đ^2}{R_x}+R_x=8\Rightarrow R_x=4\Omega\)
\(P_xmax=R_x\cdot\dfrac{U^2}{\left(R_1+R_x\right)^2}=4\cdot\dfrac{3^2}{\left(16+4\right)^2}=0,09W\)