\(a,P=\left(\dfrac{2\sqrt{x}}{\sqrt{x}+3}+\dfrac{\sqrt{x}}{\sqrt{x}-3}-\dfrac{3x+3}{x-9}\right):\left(\dfrac{2\sqrt{x}-2}{\sqrt{x}-3}-1\right)\left(x\ge0;x\ne9\right)\\ P=\dfrac{2x-6\sqrt{x}+x+3\sqrt{x}-3x-3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}:\dfrac{2\sqrt{x}-2-\sqrt{x}+3}{\sqrt{x}-3}\\ P=\dfrac{-3\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\cdot\dfrac{\sqrt{x}-3}{\sqrt{x}+1}\\ P=\dfrac{-3}{\sqrt{x}+3}\)
\(c,\sqrt{x}+3\ge3\Leftrightarrow\dfrac{3}{\sqrt{x}+3}\le\dfrac{3}{3}=1\Leftrightarrow\dfrac{-3}{\sqrt{x}+3}\le-1\)
\(P_{min}=-1\Leftrightarrow x=0\)
\(P=\dfrac{2\sqrt{x}\left(\sqrt{x}-3\right)+\sqrt{x}\left(\sqrt{x}+3\right)-3x-3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}:\dfrac{2\sqrt{x}-2-\sqrt{x}+3}{\sqrt{x}-3}\left(đk:x\ge0,x\ne9\right)\)
\(=\dfrac{-3\sqrt{x}-3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}.\dfrac{\sqrt{x}-3}{\sqrt{x}+1}=\dfrac{-3\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}+1\right)}=-\dfrac{3}{\sqrt{x}+3}\)
Có: \(\sqrt{x}+3\ge3\)
\(\Rightarrow\dfrac{3}{\sqrt{x}+3}\le1\Rightarrow P=-\dfrac{3}{\sqrt{x}+3}\ge-1\)
\(minP=-1\Leftrightarrow x=0\)
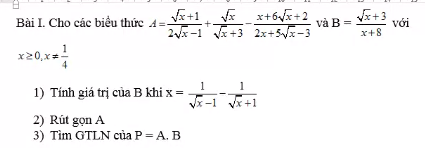
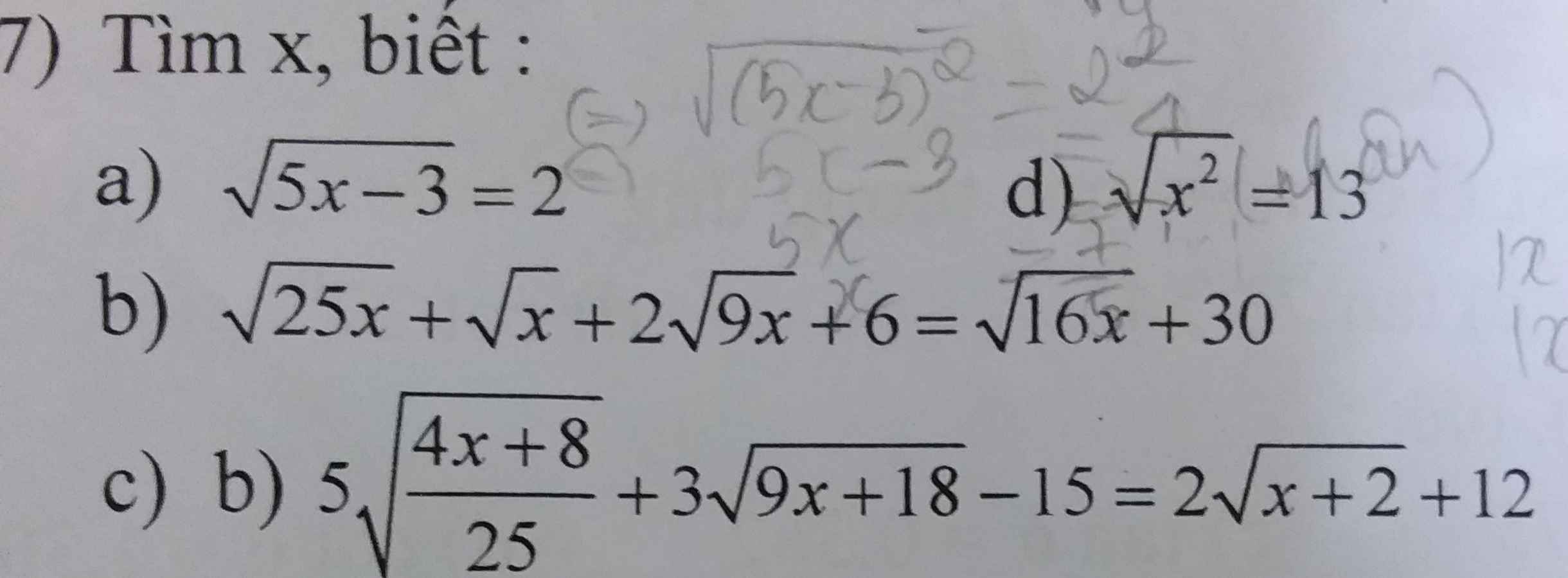
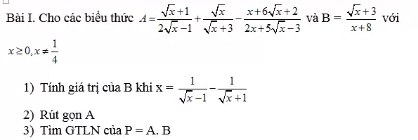
Em cần giúp câu c và d ạ, mn giúp em với em đang cần gấp