Bài 1.
a) Ta có
\(f\left(x\right)=9-x^5+4x-2x^3+x^2-7x^4\\ f\left(x\right)=-x^5-7x^4-2x^3+x^2+4x+9\)
Lại có:
\(g\left(x\right)=x^5-9+2x^2+7x^4+2x^3-3x\\ g\left(x\right)=x^5+7x^4+2x^3+2x^2-3x-9\)
b) \(h\left(x\right)=f\left(x\right)+g\left(x\right)\)
\(h\left(x\right)=\left(-x^5+x^5\right)+\left(-7x^4+7x^4\right)+\left(-2x^3+2x^3\right)+\left(x^2+2x^2\right)+\left(4x-3x\right)+\left(9-9\right)\)
\(h\left(x\right)=3x^2+x\)
c) \(h\left(x\right)=0\)
\(3x^2+x=0\)
\(x\left(3x+1\right)=0\)
TH1: \(x=0\)
TH2: \(3x+1=0\) hay \(x=-\dfrac{1}{3}\)
Vậy nghiệm của \(h\left(x\right)\) là \(x=0;x=-\dfrac{1}{3}\)
Bài 2.
a) Ta có \(\left\{{}\begin{matrix}A\left(x\right)=6x^3+5x^2\\B\left(x\right)=x^3-x^2\\C\left(x\right)=-2x^3+4x^2\end{matrix}\right.\)
\(D\left(x\right)=A\left(x\right)+B\left(x\right)-C\left(x\right)\)
\(D\left(x\right)=\left(6x^3+x^3-\left(-2x^3\right)\right)+\left(5x^2-x^2-4x^2\right)\)
\(D\left(x\right)=9x^3\)
b) \(D\left(x\right)=0\)
\(9x^3=0\\ x^3=0\\ x=0\)
Vậy nghiệm của đa thức \(D\left(x\right)\) là \(x=0\).




 giúp em 3 bài này với ạ em đang cần gấp chiều em hc ròi ạ ai làm đc bài nào thì gửi luôn giúp em ạ
giúp em 3 bài này với ạ em đang cần gấp chiều em hc ròi ạ ai làm đc bài nào thì gửi luôn giúp em ạ giúp em với ạ em đang cần gấp ạ. Bài nào làm đc trc thì làm trc giúp em với ạ
giúp em với ạ em đang cần gấp ạ. Bài nào làm đc trc thì làm trc giúp em với ạ
 Giúp em bài 4 với cả bài 5 với ạ
Giúp em bài 4 với cả bài 5 với ạ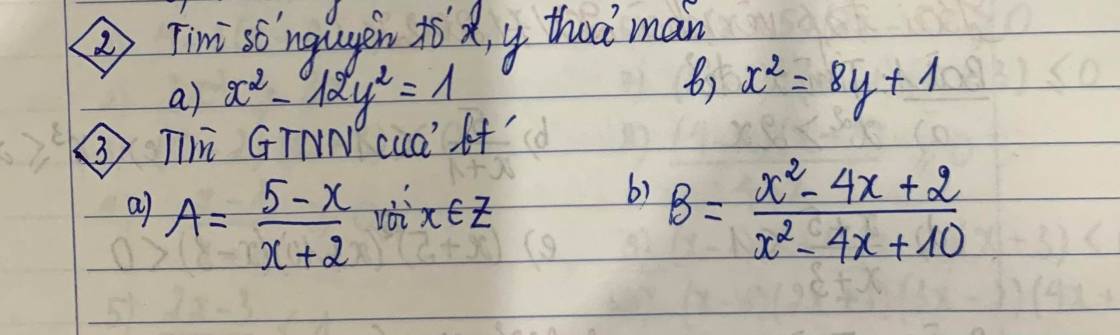
 MNG GIÚP EM BÀI 2 VỚI Ạ EM CẢM ƠN MNG NHIỀU Ạ
MNG GIÚP EM BÀI 2 VỚI Ạ EM CẢM ƠN MNG NHIỀU Ạ

