`-` Gọi 3 lớp 7A,7B,7C tỉ lệ lần lượt với x,y,z (đk:x,y,z`∈`N)
Theo đề pài ta có:`x/5 = y/4 = z/3 ` và `x-y=3`
Áp dụng dãy tỉ số bằng nhau ta có:
`x/5 = y/4 = z/3=(x-y)/(5-4) =3/1 =3`
\(\left\{{}\begin{matrix}x=5.3=15\\y=4.3=12\\z=3.3=9\end{matrix}\right.\)
Vậy số học sinh giỏi của 3 lớp 7A,7B,7C lần lượt là 15,12,9
Lời giải:
Gọi số học sinh giỏi lớp 7A, 7B, 7C lần lượt là $a,b,c$. Theo bài ra ta có:
$\frac{a}{5}=\frac{b}{4}=\frac{c}{3}$
$a-b=3$
Áp dụng tính chất dãy tỉ số bằng nhau:
$\frac{a}{5}=\frac{b}{4}=\frac{c}{3}=\frac{a-b}{5-4}=\frac{3}{1}=3$
$\Rightarrow a=3.5=15; b=4.3=12; c=3.3=9$ (học sinh)





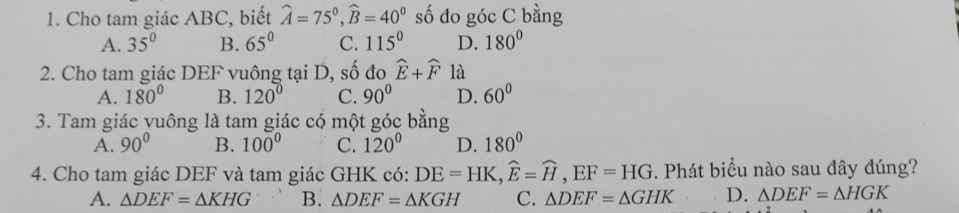

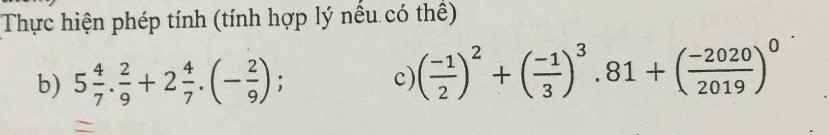

 giúp em với ạ e, đang cần gấp lắm ạ
giúp em với ạ e, đang cần gấp lắm ạ


