38.
\(y'=2x^2-8x+9=2\left(x-2\right)^2+1\ge1\)
\(\Rightarrow\) Tiếp tuyến có hệ số góc nhỏ nhất bằng 1 khi \(x_0-2=0\Rightarrow x_0=2\)
\(y\left(2\right)=-\dfrac{11}{3}\)
Phương trình d:
\(y=1\left(x-2\right)-\dfrac{11}{3}=x-\dfrac{17}{3}\)
Thay tọa độ 4 điểm của đáp án, chỉ có \(P\left(5;-\dfrac{2}{3}\right)\) thỏa mãn
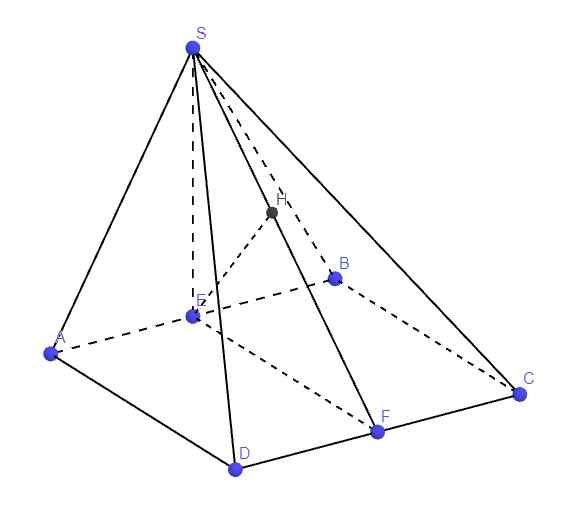
39.
Gọi E là trung điểm AB, F là trung điểm CD
Từ E kẻ EH vuông góc SF (H thuộc SF)
Do tam giác SAB đều \(\Rightarrow SE\perp AB\Rightarrow SE\perp\left(ABCD\right)\)
\(\Rightarrow SE\perp CD\)
\(EF||AD\Rightarrow EF\perp CD\)
\(\Rightarrow CD\perp\left(SEF\right)\) \(\Rightarrow CD\perp EH\)
\(\Rightarrow EH\perp\left(SCD\right)\Rightarrow EH=d\left(E;\left(SCD\right)\right)\)
Lai có: \(AB||CD\Rightarrow AB||\left(SCD\right)\Rightarrow d\left(A;\left(SCD\right)\right)=d\left(E;\left(SCD\right)\right)=EH\)
\(SE=\dfrac{AB\sqrt{3}}{2}=\dfrac{\sqrt{3}}{2}\) ; \(EF=AD=1\)
Hệ thức lượng: \(d=HE=\dfrac{SE.EF}{\sqrt{SE^2+EF^2}}=\dfrac{\sqrt{21}}{7}\)
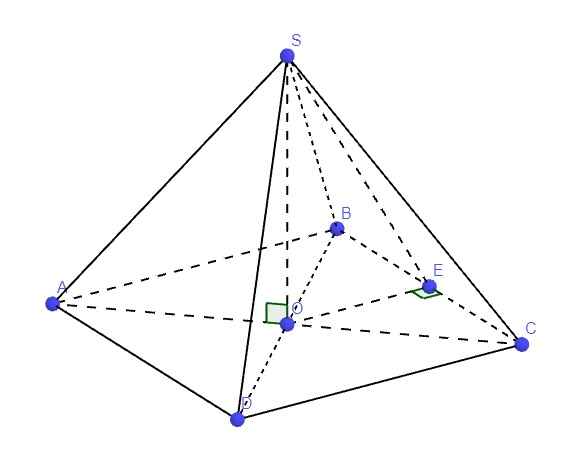
40.
Gọi E là trung điểm BC
\(\Rightarrow OE\) là đường trung bình tam giác ABC
\(\Rightarrow\left\{{}\begin{matrix}OE||AB\Rightarrow OE\perp BC\\OE=\dfrac{1}{2}AB=\dfrac{a}{2}\end{matrix}\right.\)
Do chóp đều nên \(SO\perp\left(ABCD\right)\) \(\Rightarrow SO\perp BC\)
\(\Rightarrow BC\perp\left(SOE\right)\)
Mà \(BC=\left(SBC\right)\cap\left(ABCD\right)\Rightarrow\widehat{SEO}\) là góc giữa (SBC) và (ABCD)
\(tan\widehat{SEO}=\dfrac{SO}{OE}=\sqrt{3}\)
\(\Rightarrow\widehat{SEO}=60^0\)