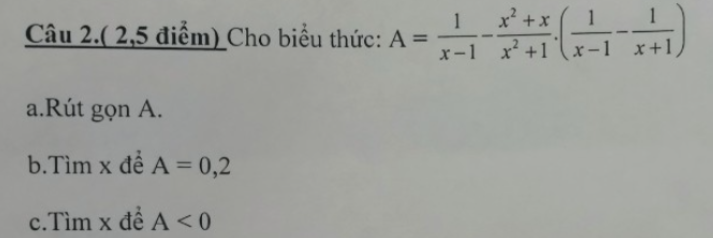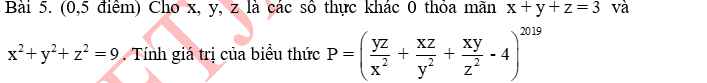giúp e đi em xin mng đấy ạ
\(1,=\left(x-3\right)^2\\ 2,=\left(5+x\right)^2\\ 3,=\left(\dfrac{1}{2}x+2b\right)^2\\ 4,=\left(\dfrac{1}{3}-y^4\right)^2\\ 5,=\left(x+2y\right)\left(x^2-2xy+4y^2\right)\\ 6,=\left(2y-5\right)\left(4y^2+10y+25\right)\\ 7,=\left(a^2-b\right)\left(a^4+a^2b+b^2\right)\\ 8,=\left(x-5\right)^2\\ 9,=8\left(x^3-\dfrac{1}{64}\right)=8\left(x-\dfrac{1}{4}\right)\left(x^2+\dfrac{1}{4}x+\dfrac{1}{16}\right)\)
Bn dùng hằng đẳng thức đáng nhớ nhé.
Thêm một chút kiên thức về bài:
\(\left(\dfrac{a}{b}\right)^2=\dfrac{a^2}{b^2}\)
\(a^{xy}=\left(a^x\right)^y\)
\(8,=\left(3x+2-2\right)\left(3x+2+2\right)=3x\left(3x+4\right)\\ 9,=\left(2x-5y\right)\left(2x+5y\right)\\ 10,=\left(2x-7\right)\left(2x+7\right)\\ 11,=\left(2z+3\right)\left(4z^2-6z+9\right)\\ 12,=\left(\dfrac{3}{5}x^2-\dfrac{1}{2}\right)\left(\dfrac{3}{5}x^2+\dfrac{1}{2}\right)\\ 13,=\left(x^{16}-1\right)\left(x^{16}+1\right)=\left(x^8-1\right)\left(x^8+1\right)\left(x^{16}+1\right)\\ =\left(x-1\right)\left(x+1\right)\left(x^2+1\right)\left(x^4+1\right)\left(x^8+1\right)\left(x^{16}+1\right)\\ 14,=\left(2x+1\right)^2\\ 15,=\left(x-10\right)^2\\ 16,=\left(y^2-7\right)^2\)
giúp e vs 
