ĐK: \(x>0;x\ne1\)
\(C=\left(\sqrt{x}-\dfrac{1}{\sqrt{x}}\right):\left(\dfrac{\sqrt{x}-1}{\sqrt{x}}+\dfrac{1-\sqrt{x}}{x+\sqrt{x}}\right)\)
\(=\dfrac{x-1}{\sqrt{x}}:\left(\dfrac{\left(\sqrt{x}-1\right)^2\left(\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)\left(\sqrt{x+1}\right)}-\dfrac{\left(\sqrt{x}-1\right)^2}{\sqrt{x}\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\right)\)
\(=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}}:\dfrac{\left(\sqrt{x}-1\right)^2\left(\sqrt{x}+1\right)-\left(\sqrt{x}-1\right)^2}{\sqrt{x}\left(\sqrt{x}-1\right)\left(\sqrt{x+1}\right)}\)
\(=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}}.\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)^2\left(\sqrt{x}+1\right)-\left(\sqrt{x}-1\right)^2}\)
\(=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)^2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)-\left(\sqrt{x}-1\right)}\)
\(=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)^2}{\sqrt{x}\left(\sqrt{x}-1\right)}\)
\(=\dfrac{\left(\sqrt{x}+1\right)^2}{\sqrt{x}}=\sqrt{x}+\dfrac{1}{\sqrt{x}}+2\ge2\sqrt{\sqrt{x}.\dfrac{1}{\sqrt{x}}}+2=4\)
Đẳng thức không xảy ra nên \(C>4\).
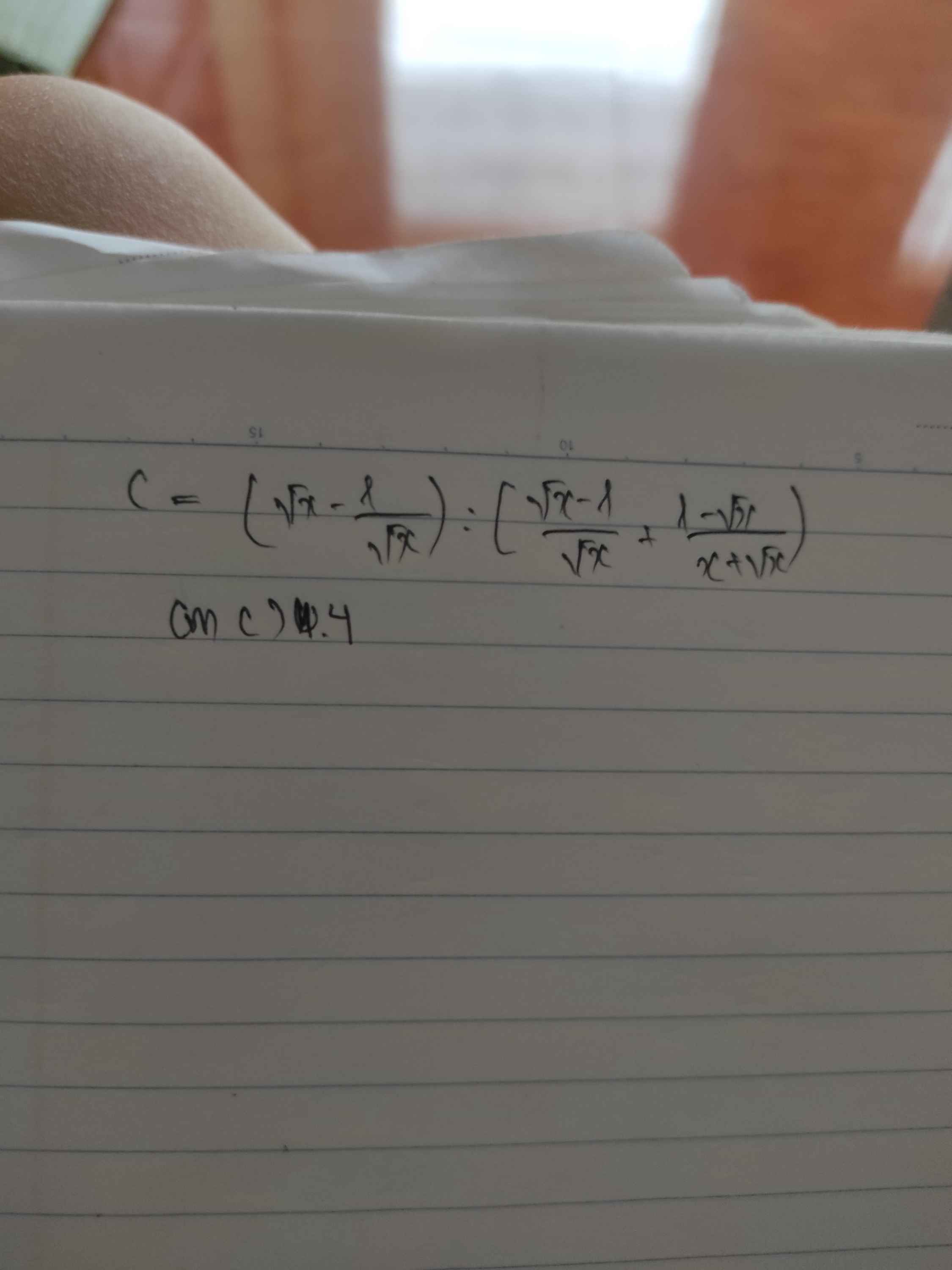
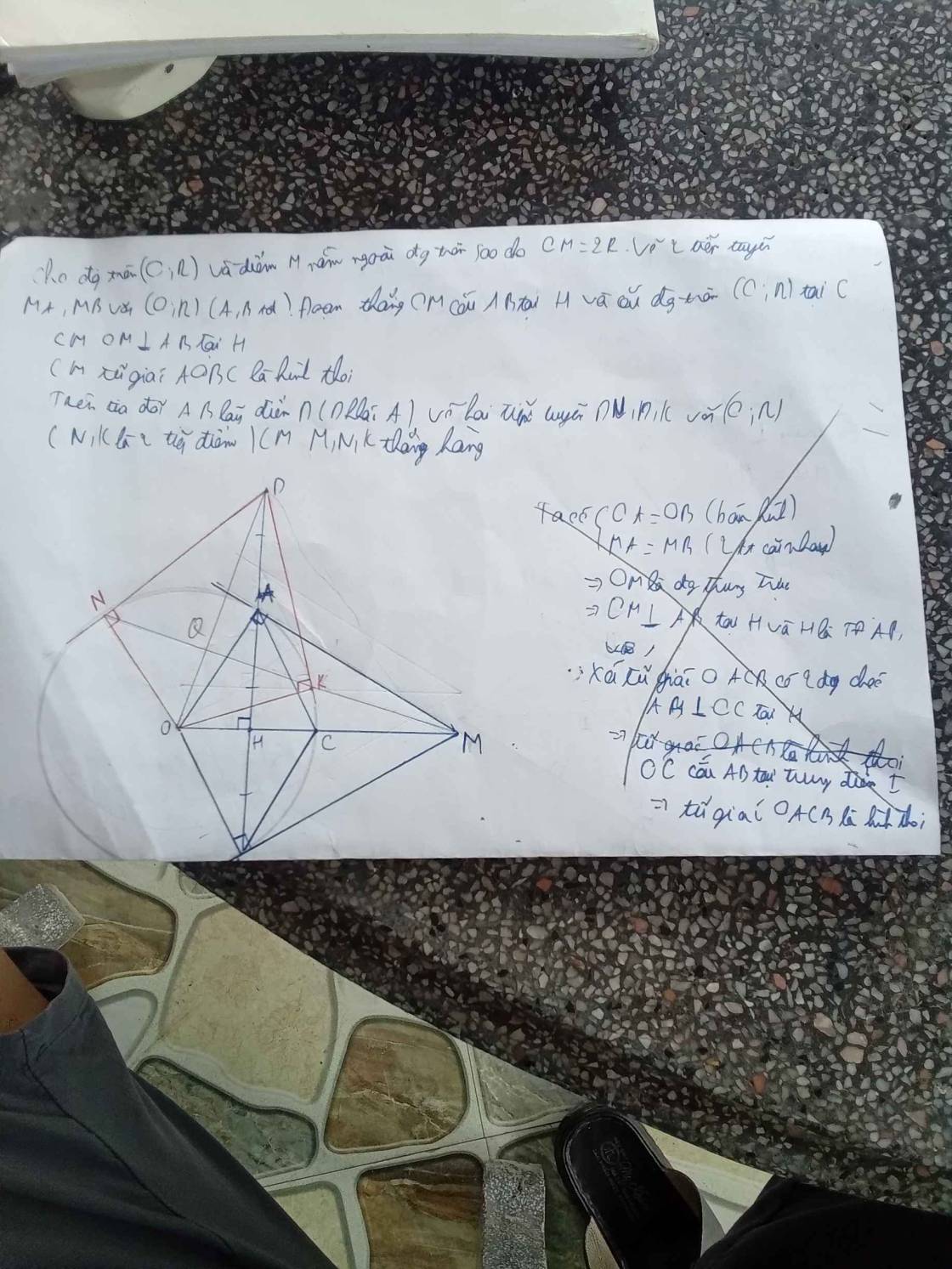
Chứng minh 2 ý đó giúp e vs ạ e đang cần gấp