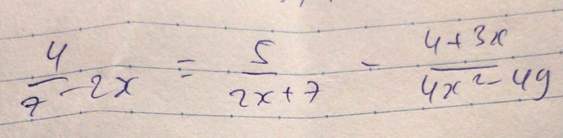Bài 45:
a. $x^3-5x^2+8x-4=x^2(x-1)-4x(x-1)+4(x-1)=(x-1)(x^2-4x+4)$
$=(x-1)(x-2)^2$
b. $x^3-3x+2=x^2(x-1)+x(x-1)-2(x-1)=(x-1)(x^2+x-2)$
$=(x-1)[x(x-1)+2(x-1)]=(x-1)(x-1)(x+2)=(x-1)^2(x+2)$
c. $x^3-5x^2+3x+9=x^2(x+1)-6x(x+1)+9(x+1)$
$=(x+1)(x^2-6x+9)=(x+1)(x-3)^2$
d. $x^3+8x^2+17x+10=x^2(x+1)+7x(x+1)+10(x+1)$
$=(x+1)(x^2+7x+10)=(x+1)[x(x+2)+5(x+2)]=(x+1)(x+2)(x+5)$
e. $x^3+3x^2+6x+4=x^2(x+1)+2x(x+1)+4(x+1)=(x+1)(x^2+2x+4)$
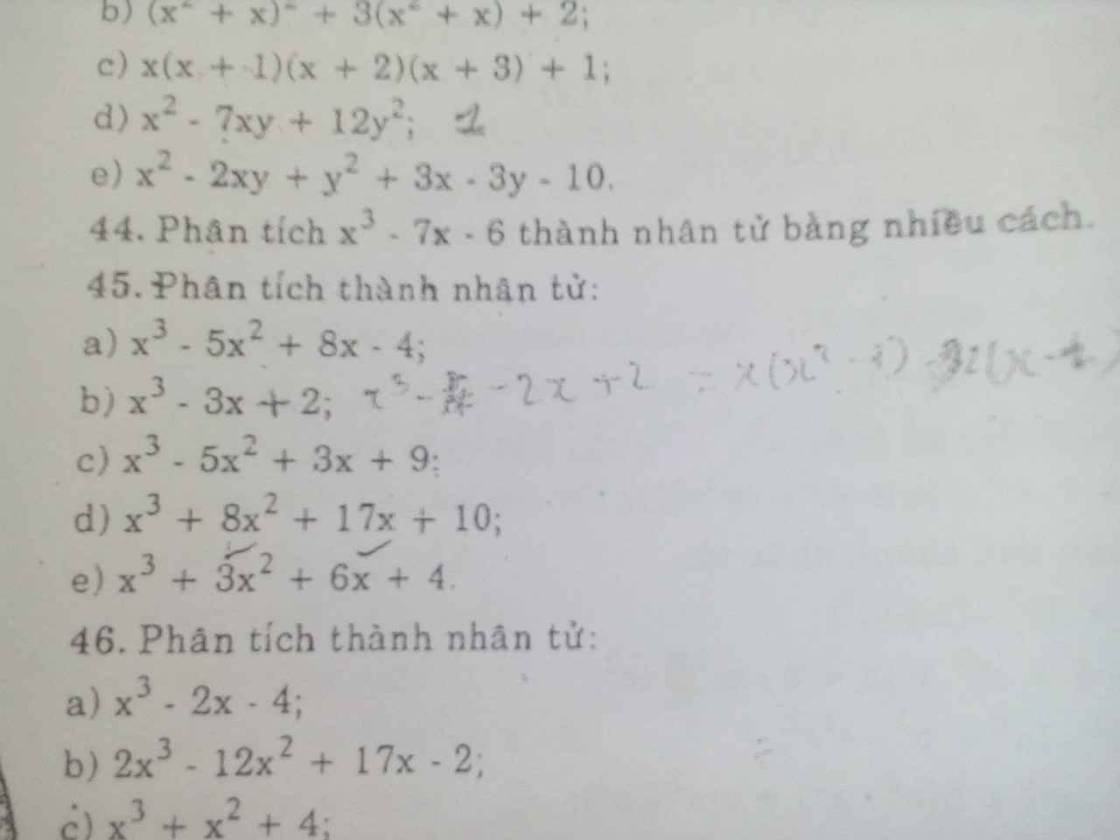

 Giúp e bài 2 thôi ạ bài 1 e làm r ạ! Mong mn giúp e, e cần gấp ạ!
Giúp e bài 2 thôi ạ bài 1 e làm r ạ! Mong mn giúp e, e cần gấp ạ!