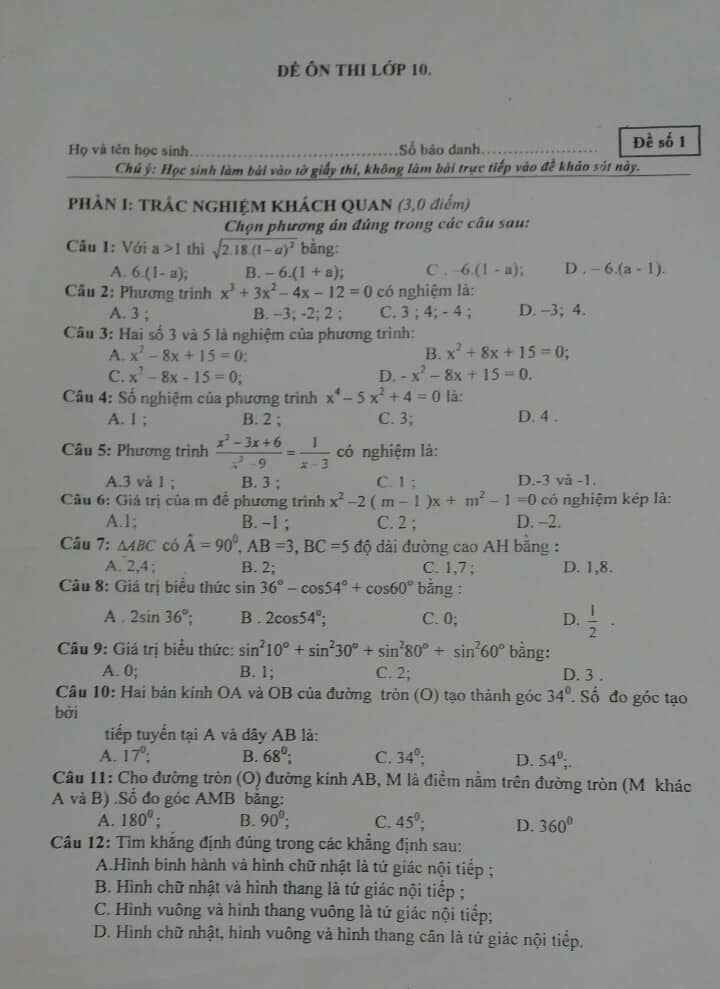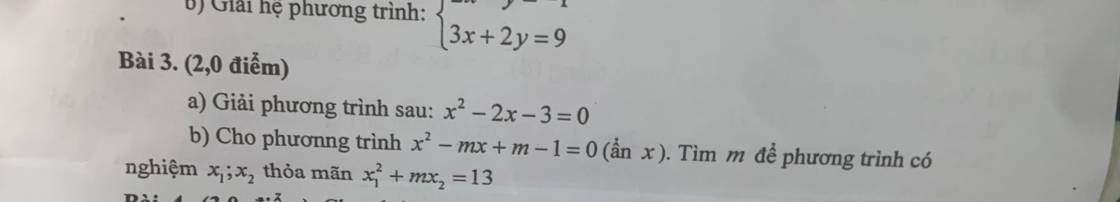\(A=\sqrt[3]{1+\dfrac{\sqrt{84}}{9}}+\sqrt[3]{1-\dfrac{\sqrt{84}}{9}}=a+b\)
Áp dụng hằng đẳng thức đáng nhớ \(\left(a+b\right)^3=a^3+b^3+3ab\left(a+b\right)\)
\(2=\left(\sqrt[3]{1+\dfrac{\sqrt{84}}{9}}\right)^3+\left(\sqrt[3]{1-\dfrac{\sqrt{84}}{9}}\right)^3=a^3+b^3\)
\(3\left(\sqrt[3]{1+\dfrac{\sqrt{84}}{9}}+\sqrt[3]{1-\dfrac{\sqrt{84}}{9}}\right).\sqrt[3]{1+\dfrac{\sqrt{84}}{9}}.\sqrt[3]{1-\dfrac{\sqrt{84}}{9}}=3\left(a+b\right)ab\)
\(\sqrt[3]{1+\dfrac{\sqrt{84}}{9}}.\sqrt[3]{1-\dfrac{\sqrt{84}}{9}}=\sqrt[3]{\left(1+\dfrac{\sqrt{84}}{9}\right)\left(1-\dfrac{\sqrt{84}}{9}\right)}=\sqrt[3]{1-\dfrac{84}{81}}\)
\(\Rightarrow A^3=2+3A\sqrt[3]{1-\dfrac{84}{81}}\)





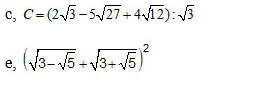
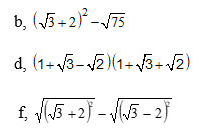 các bạn giải hộ mik mấy câu này vs mik đag cần gấp
các bạn giải hộ mik mấy câu này vs mik đag cần gấp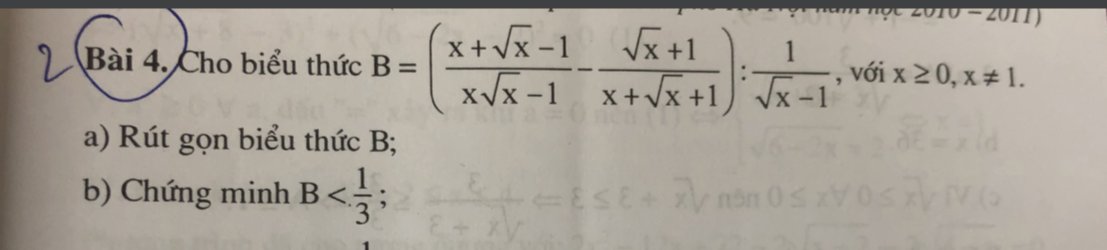

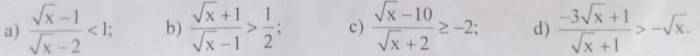 giải câu c và d hộ mik vs
giải câu c và d hộ mik vs