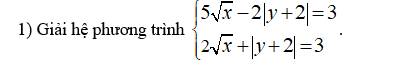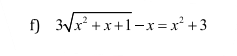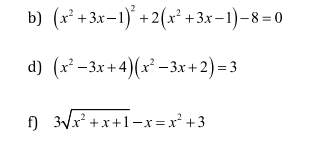Đặt $|x-1|=a,\sqrt{y+2}=b(x\in \Bbb R, y\ge -2)$
$\Rightarrow \begin{cases}2a-b=4\\a+3b=9\end{cases}\\\Leftrightarrow \begin{cases}2a=b+4\\a+3b=9\end{cases}\\\Leftrightarrow \begin{cases}a=\dfrac{b+4}{2}\\a+3b=9\end{cases}\\\Leftrightarrow\begin{cases}a=\dfrac{b+4}{2}\\\dfrac{b+4}{2}+3b=9\end{cases}\\\Leftrightarrow\begin{cases}a=\dfrac{b+4}{2}\\b+4+6b=18\end{cases}\\\Leftrightarrow\begin{cases}a=\dfrac{b+4}{2}\\7b=14\end{cases}\\\Leftrightarrow\begin{cases}a=\dfrac{b+4}{2}\\b=2\end{cases}\\\Leftrightarrow\begin{cases}a=3\\b=2(TM)\end{cases}\\\Leftrightarrow\begin{cases}|x-1|=3\\\sqrt{y+2}=2\end{cases}\\\Leftrightarrow\begin{cases}\left[\begin{array}{1}x-1=3\\x-1=-3\end{array}\right.\\y+2=4\end{cases}\\\Leftrightarrow\begin{cases}\left[\begin{array}{1}x=4\\x=-2\end{array}\right.\\y=2(TM)\end{cases}$
Vậy $(x,y)=\{(4;2);(-2;2)\}$



 p
p