Các câu hỏi tương tự
Cho hàm số
y
4
x
3
-
6
x
2
+
1
có đồ thị là đường cong trong hình dưới đây. Khi đó phương trình
4
4
x
3
-
6
x...
Đọc tiếp
Cho hàm số y = 4 x 3 - 6 x 2 + 1 có đồ thị là đường cong trong hình dưới đây.
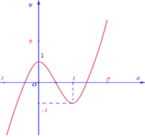
Khi đó phương trình 4 4 x 3 - 6 x 2 + 1 3 - 6 4 x 3 - 6 x 2 + 1 + 1 = 0 có bao nhiêu nghiệm thực.
A. 9
B. 6
C. 7
D. 3
Cho hàm số
y
4
x
3
-
6
x
2
+
1
có đồ thị là đường cong trong hình dưới đây. Khi đó phương trình
4
4
x
3
-
6
x...
Đọc tiếp
Cho hàm số y = 4 x 3 - 6 x 2 + 1 có đồ thị là đường cong trong hình dưới đây.
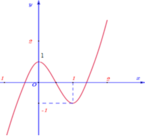
Khi đó phương trình 4 4 x 3 - 6 x 2 + 1 3 - 6 4 x 3 - 6 x 2 + 1 2 + 1 = 0 có bao nhiêu nghiệm thực.
A. 9
B. 6
C. 7
D. 3
Có bao nhiêu giá trị nguyên của m để phương trình sau vô nghiệm
x
6
+
3
x
5
+
6
x
4
−
m
x
3
+
6
x
2
+
3
x
+
1
0
A. Vô số B. 26 C. 27 D. 28
Đọc tiếp
Có bao nhiêu giá trị nguyên của m để phương trình sau vô nghiệm x 6 + 3 x 5 + 6 x 4 − m x 3 + 6 x 2 + 3 x + 1 = 0
A. Vô số
B. 26
C. 27
D. 28
Gọi M là giá trị lớn nhất của hàm số
f
(
x
)
6
x
2
-
6
x
+
12
+
6
x
-
x
2
-
4
. Tính tích các nghiệm của phương trình f(x)M. A. -6 B. 3 C. -3 D. 6
Đọc tiếp
Gọi M là giá trị lớn nhất của hàm số f ( x ) = 6 x 2 - 6 x + 12 + 6 x - x 2 - 4 . Tính tích các nghiệm của phương trình f(x)=M.
A. -6
B. 3
C. -3
D. 6
Gọi M là giá trị lớn nhất của hàm số
f
(
x
)
6
x
2
-
6
x
+
12
+
6
x
-
x
2
-
4
. Tính tích các nghiệm của phương trình f(x) M. A. -6 B. 3 C. -3 D. 6
Đọc tiếp
Gọi M là giá trị lớn nhất của hàm số f ( x ) = 6 x 2 - 6 x + 12 + 6 x - x 2 - 4 . Tính tích các nghiệm của phương trình f(x) = M.
A. -6
B. 3
C. -3
D. 6
Biện luận theo tham số m số nghiệm của phương trình: x 4 - 6 x 2 + 3 = m .
Giải phương trình
log
3
(
x
-
4
)
0
. A. x1 B. x6 C. x5 D. x4
Đọc tiếp
Giải phương trình log 3 ( x - 4 ) = 0 .
A. x=1
B. x=6
C. x=5
D. x=4
Giải phương trình f'(x - 1) > 0.
Cho
f
x
x
-
3
x
. Giải phương trình f(x)0 A. 0 B. ln3 C.
log
1
3
ln
3
D.
x
3
ln
3
Đọc tiếp
Cho f x = x - 3 x . Giải phương trình f'(x)=0
A. 0
B. ln3
C. log 1 3 ln 3
D. x = 3 ln 3

